题目内容
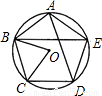
 如图,若五边形ABCDE是⊙O的内接正五边形,则∠BOC=
如图,若五边形ABCDE是⊙O的内接正五边形,则∠BOC=72°
72°
,∠ABE=36°
36°
,∠ADC=72°
72°
,∠ABC=108°
108°
.分析:由五边形ABCDE为正五边形,可得∠BOC为周角的五分之一,求出即可;由内角和定理求出五边形的内角和,根据五边形的五个内角相等,求出每一个内角,可得到∠AED,∠CDE及∠ABC都相等,并求出度数,再由正五边形的边长相等可得AE=DE,得到三角形AED为等腰三角形,由顶角∠AED的度数求出底角∠ADE的度数,根据同弧所对的圆周角的相等可得∠ABE与∠ADE的度数相等,进而求出∠ABE的度数,再由∠CDE-∠ADE可得出∠ADC的度数.
解答:解:∵五边形ABCDE是⊙O的内接正五边形,
∴∠BOC=360°×
=72°,
又正五边形的内角和为(5-2)×180°=540°,
∴∠AED=∠CDE=∠ABC=540°×
=108°,AE=DE,
∴∠ADE=∠DAE=
(180°-108°)=36°,
又圆周角∠ABE与∠ADE所对的弧都为
,
∴∠ABE=∠ADE=36°,
又∠CDE=108°,∠ADE=36°,
∴∠ADC=∠CDE-∠ADE=108°-36°=72°.
故答案为:72°;36°;72°;108°
∴∠BOC=360°×
| 1 |
| 5 |
又正五边形的内角和为(5-2)×180°=540°,
∴∠AED=∠CDE=∠ABC=540°×
| 1 |
| 5 |
∴∠ADE=∠DAE=
| 1 |
| 2 |
又圆周角∠ABE与∠ADE所对的弧都为
 |
| AE |
∴∠ABE=∠ADE=36°,
又∠CDE=108°,∠ADE=36°,
∴∠ADC=∠CDE-∠ADE=108°-36°=72°.
故答案为:72°;36°;72°;108°
点评:此题考查了正五边形的性质,圆周角定理,内角和定理,等腰三角形的性质,利用了转化的思想,结合图形找出已知条件与所求角的关系是解本题的关键.

练习册系列答案
相关题目
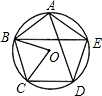
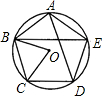 如图,若五边形ABCDE是⊙O的内接正五边形,则∠BOC=________,∠ABE=________,∠ADC=________,∠ABC=________.
如图,若五边形ABCDE是⊙O的内接正五边形,则∠BOC=________,∠ABE=________,∠ADC=________,∠ABC=________.