题目内容
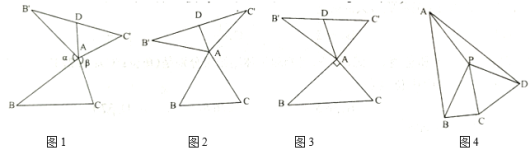
【题目】我们定义：如图1，在
中，把
绕点
顺时针旋转
得到
，把
绕点逆时针旋转
得到
，连接
．当
时，我们称
是的“旋补三角形”，边上的中线
叫做的“旋补中线”．
（特例感知）
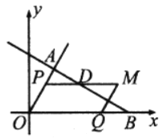
（1）在图2，图3中，是的“旋补三角形”，是的“旋补中线”．
①如图2，当为等边三角形，且
时，则长为 ．
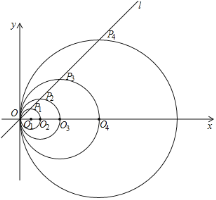
②如图3，当
，且
时，则长为 ．
（猜想论证）
（2）在图1中，当为任意三角形时，猜想与
的数量关系，并给予证明．（如果你没有找到证明思路，可以考虑延长或延长
，……）
（拓展应用）
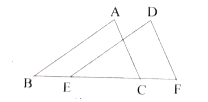
（3）如图4，在四边形
中，
，
，
，以
为边在四边形内部作等边
，连接
，
．若
是
的“旋补三角形”，请直接写出的“旋补中线”长及四边形的边长．
【答案】（1）①
，②
；（2）
，见解析；（3）
，
【解析】
（1）①由旋补三角形的概念可证明△ADB′是含有30°是直角三角形，可得AD=
BC即可解决问题；
②首先证明△BAC≌△B′AC′，根据直角三角形斜边中线定理即可解决问题；
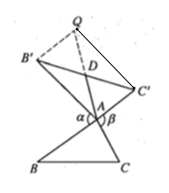
（2）结论：AD=BC．如图1中，延长AD到Q，使得AD=DQ，连接B′Q，C′Q，首先证明四边形AC′QB′是平行四边形，再证明△BAC≌△AB′Q，即可解决问题；
（3）由
，
是等边三角形可得
，由旋补三角形的概念可得
，PB=PA，进而求出PB的长，再根据勾股定理就可求出BC的长，由（2）的结论即可求出旋补中线PE的长和AD的长．
解：（1）①∵
是
的“旋补三角形”，
∴
，
，
,
∵为等边三角形，且
，
∴
，
，
∴
是等腰三角形，
，
∴AD⊥
，
，
∴AD=3，
②∵是的“旋补三角形”，
∴，，,
∵
，
∴
，
∴
，
∴
，
∵AD为中线，
∴
；
（2)猜想：
如图，延长
至Q，使
．
∵是的“旋补中线”，
．
四边形
是平行四边形，
，
．
由定义可知
，
，
，
，
，
．
∵
，；
（3）过点P作PE⊥AB，取AD的中点F，连接PF，延长DP，过点A作AM⊥DM，如图，
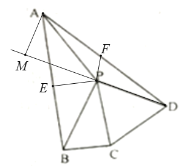
∵，△PCD是等边三角形，
∴，
∵CD=6，
∴PC=CD=PD=6，
∵
是
的“旋补三角形”，
∴，PB=PA，
，
∴△PAB是等腰三角形，
，
∵PE⊥AB，
∴EB=EA
∵AB=12，
∴BE=6，
，
在△PBC中，由勾股定理得，
，
由（2）可知，
，
∴
，
∵，
∴
,
∵
,
∴
，
∴
，
，
∴MD=12，
在△AMD中，由勾股定理得，
∴
．
