题目内容
【题目】如图,正方形ABCD的边AB在数轴上,数轴上点A表示的数为-1,正方形ABCD的面积为16.
(1)数轴上点B表示的数为 ;
(2)将正方形ABCD沿数轴水平移动,移动后的正方形记为![]() ,移动后的正方形
,移动后的正方形![]() 与原正方形ABCD重叠部分的面积记为S.
与原正方形ABCD重叠部分的面积记为S.
① 当S =4时,画出图形,并求出数轴上点![]() 表示的数;
表示的数;
② 设正方形ABCD的移动速度为每秒2个单位长度,点E为线段![]() 的中点,点F在线段
的中点,点F在线段![]() 上,且
上,且![]() . 经过
. 经过![]() 秒后,点E,F所表示的数互为相反数,直接写出
秒后,点E,F所表示的数互为相反数,直接写出![]() 的值.
的值.

【答案】(1)-5;(2)– 4或2;(3)t=4.
【解析】试题分析:(1)、根据正方形的面积得出AB=4,根据点A所表示的数得出点B所表示的数;(2)、①、根据题意得出矩形的一边长为4,要使面积为4,则另一边长为1,然后根据向左移动和向右移动两种情况分别画出图形得出答案;②、用含t的代数式分别表示出点E和点F所表示的数,然后根据互为相反数的两个数的和为零列出方程得出答案.
试题解析:解:(1)、–5;
(2)、∵正方形ABCD的面积为16,∴边长为4.
当S=4时,①若正方形ABCD向左平移,如图1,
重叠部分中的A'B =1,∴AA'=3.
则点A'表示–1–3= – 4.
②若正方形ABCD向右平移,如图2,
重叠部分中的AB'=1,∴AA'=3.
则点A'表示–1+3= 2,∴点A'表示的数为– 4或2.
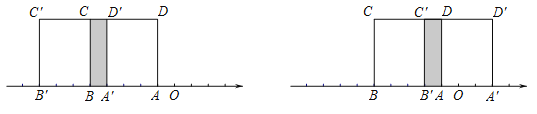
图1 图2
(3)t=4.

练习册系列答案
相关题目