Question

在初三毕业晚会上，同学们表演哪一类型的节目由自己摸球来决定．在一个不透明的口袋中，装有除标号外其它完全相同的A、B、C三个小球，表演节目前，先从袋中摸球一次（摸球后又放回袋中），如果摸到的是A球，则表演唱歌；如果摸到的是B球，则表演跳舞；如果摸到的是C球，则表演朗诵．
（1）若小明要表演一个节目，则他表演的节目是跳舞的概率是________．
（2）若小芳要表演两个节目，小芳认为她表演的节目至少有一个是跳舞的概率是（1）问中小明的两倍，你赞同她的观点吗？请用树状图或列表法进行分析说明．

Answer 1

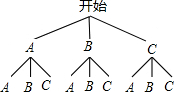解：（1）∵一共有A、B、C三种等可能的结果，
小明表演的节目是跳舞的只有1种情况，
∴他表演的节目是跳舞的概率是；

（2）画树状图得：
∴一共有9种等可能的结果，
小芳认表演的节目至少有一个是跳舞的有5种，
∴小芳认表演的节目至少有一个是跳舞的概率为：，
∵＜×2，
∴我赞同她的观点．
分析：（1）利用概率公式直接求解即可求得答案；
（2）依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式即可求出该事件的概率，则可求知小芳认为她表演的节目至少有一个是跳舞的概率是（1）问中小明的两倍的观点是否正确．
点评：本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．游戏双方获胜的概率相同，游戏就公平，否则游戏不公平．用到的知识点为：概率=所求情况数与总情况数之比．