题目内容
如下图,△ABC中,∠B、∠C的平分线BM、CN相交于点P.求证:AP平分∠BAC.
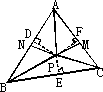
当我们把问题解决之后会发现:一个三角形的三个角的平分线都相交于一点,并且这个点到三角形的三条边的距离相等.
由此我们就可以得出三角形的另一个面积公式.
答案:
解析:
解析:
|
探索:由例题可以得到:△ABC的三条角平分线必交于点P.过点P作PD⊥AB,PE⊥BC,PF⊥AC,垂足分别为D、E、F. 由图可以知道:S△APB= 这样我们就可以得到三角形的另一个面积公式:S△ABC= 当我们探索了三角形的这个面积公式后,对于有关三角形的面积问题就有了两种计算方法,解题时要结合具体的情况选择合适的公式进行计算. |

练习册系列答案
相关题目
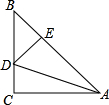 如下图,△ABC中,∠C=90°,∠B=45°,AD是角平分线,DE⊥AB于E,则下列结论不正确的是( )
如下图,△ABC中,∠C=90°,∠B=45°,AD是角平分线,DE⊥AB于E,则下列结论不正确的是( )| A、AC=AE | B、CD=DE | C、CD=DB | D、AB=AC+CD |
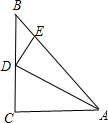 如下图,△ABC中,∠C=90°,∠B=45°,AB=
如下图,△ABC中,∠C=90°,∠B=45°,AB= 12、如下图,△ABC中,AB的垂直平分线交AC于D,如果AC=5cm,BC=4cm,那么△DBC的周长是( )
12、如下图,△ABC中,AB的垂直平分线交AC于D,如果AC=5cm,BC=4cm,那么△DBC的周长是( )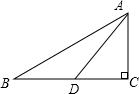 如下图,△ABC中,∠C=90°,AD是BC边的中线,∠ABC=α,∠ADC=β,则tanα与tanβ之间的关系是
如下图,△ABC中,∠C=90°,AD是BC边的中线,∠ABC=α,∠ADC=β,则tanα与tanβ之间的关系是