题目内容
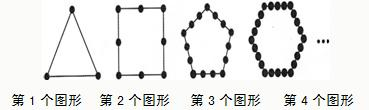
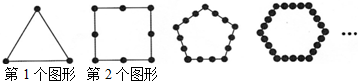
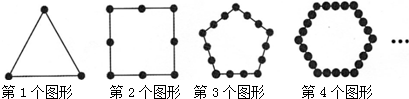
如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第12个图形需要黑色棋子的个数是( )


分析:图①中棋子数:1×3,图②中棋子数:2×4,图③中棋子数:3×5,图④中棋子数:4×6,…依此类推:第12个图形中棋子数:12×14=168.
解答:解:结合图形,
发现:第1个图形中黑色棋子的个数是2×3-3;
第2个图形中黑色棋子的个数是3×4-4,
∴第12个图形需要黑色棋子的个数是13×14-14=168(个).
故选D.
发现:第1个图形中黑色棋子的个数是2×3-3;
第2个图形中黑色棋子的个数是3×4-4,
∴第12个图形需要黑色棋子的个数是13×14-14=168(个).
故选D.
点评:考查了规律型:图形的变化,本题是一道探索规律题,本题的解题规律是边数每增加一条,每条边也增加一个棋子,用边数乘以每边上的棋子数减1的积,即棋子总数.

练习册系列答案
相关题目