Question

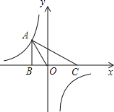
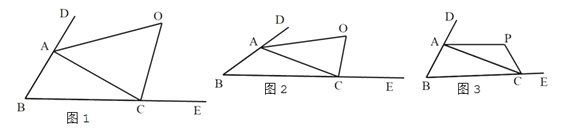
【题目】（1）如图1．在△ABC中，∠B=60°，∠DAC和∠ACE的角平分线交于点O，则∠O=　　　　 °，

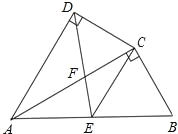
（2）如图2，若∠B=α，其他条件与（1）相同，请用含α的代数式表示∠O的大小；

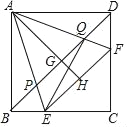
（3）如图3，若∠B=α，，则∠P=　　　　 （用含α的代数式表示）．

Answer 1

【答案】（1）∠O=60°；（2）90°－；（3）

【解析】

（1）由题意利用角平分线的性质和三角形内角和为180°进行分析求解；

（2）根据题意设∠BAC=β，∠ACB=γ，则α+β+γ=180°，利用角平分线性质和外角定义找等量关系，用含α的代数式表示∠O的大小；

（3）利用（2）的条件可知n=2时，∠P=，再将2替换成n即可分析求解.

解：（1）因为∠DAC和∠ACE的角平分线交于点O，且∠B=60°，

所以，

有∠O=60°.

（2）设∠BAC=β，∠ACB=γ，则α+β+γ=180°

∵∠ACE是△ABC的外角，

∴∠ACE=∠B+∠BAC=α+β

∵CO平分∠ACE

同理可得：

∵∠O+∠ACO+∠CAO=180°，

∴

；

（3）∵∠B=α，，

由（2）可知n=2时，有∠P==，将2替换成n即可，

∴.