题目内容
【题目】我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A(体操)、B(乒乓球)、C(毽球)、D(跳绳)四项活动.为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图。
请根据统计图回答下列问题:
(1)这次被调查的学生共有_____人;
(2)请将统计图2补充完整;
(3)统计图1中B项目对应的扇形的圆心角是 _____度;
(4)已知该校共有学生1000人,根据调查结果估计该校喜欢体操的学生有_____人.


【答案】 400 108 100
【解析】分析:(1)根据C类的人数除以C类人数所占的百分比,即可求出总人数;(2)分别求得A类的人数和D类的人数,从而补全条形统计图即可;(2)利用喜欢B类项目的学生所占的百分比乘以360°即可得B项目对应的扇形的圆心角的度数;(4)用总人数乘以喜欢体操的学生所占的百分比即可得答案.
详解:
(1)这次被调查的学生共有160÷40%=400(人),
故答案为:400;
(2)D项目的人数为400×20%=80(人),
则A项目的人数为400-(120+160+80)=40(人),
补全图形如下: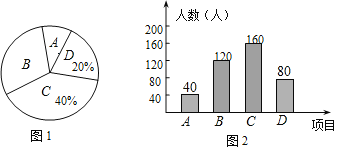
(3)统计图1中B项目对应的扇形的圆心角是![]() ×360°=108°,
×360°=108°,
故答案为:108;
(4)根据调查结果估计该校喜欢体操的学生有1000×![]() =100(人),
=100(人),
故答案为:100.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案【题目】我们规定:有理数xA用数轴上点A表示,xA叫做点A在数轴上的坐标;有理数xB用数轴上点B表示,xB叫做点B在数轴上的坐标.|AB|表示数轴上的两点A,B之间的距离.
(1)借助数轴,完成下表:
xA | xB | xA﹣xB | |AB| |
3 | 2 | 1 | 1 |
1 | 5 |
|
|
2 | ﹣3 |
|
|
﹣4 | 1 |
|
|
﹣5 | ﹣2 |
|
|
﹣3 | ﹣6 |
|
|
(2)观察(1)中的表格内容,猜想|AB|= ;(用含xA,xB的式子表示,不用说理)
(3)已知点A在数轴上的坐标是﹣2,且|AB|=8,利用(2)中的结论求点B在数轴上的坐标.