Question

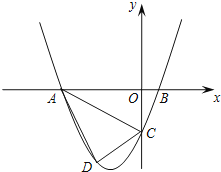
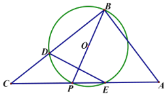
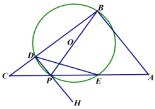
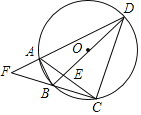
【题目】如图，四边形ABCD为圆内接四边形，对角线AC、BD交于点E，延长DA、CB交于点F．

（1）求证：△FBD∽△FAC；

（2）如果BD平分∠ADC，BD＝5，BC＝2，求DE的长；

（3）如果∠CAD＝60°，DC＝DE，求证：AE＝AF．

Answer 1

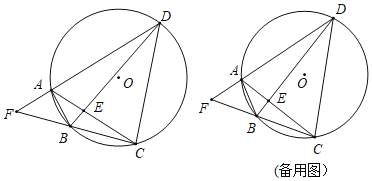
【答案】（1）见解析；（2）；（3）见解析

【解析】

（1）可得出∠ADB=∠ACB，∠AFC=∠BFD，则结论得证；

（2）证明△BEC∽△BCD，可得，可求出BE长，则DE可求出；

（3）根据圆内接四边形的性质和三角形的内角和定理进行证明AB=AF；根据等腰三角形的判定与性质和圆周角定理可证明AE=AB，则结论得出．

（1）证明：∵∠ADB＝∠ACB，∠AFC＝∠BFD，

∴△FBD∽△FAC；

（2）解：∵BD平分∠ADC，

∴∠ADB＝∠BDC，

∵∠ADB＝∠ACB，

∴∠ACB＝∠BDC，

∵∠EBC＝∠CBD，

∴△BEC∽△BCD，

∴，

∴，

∴BE＝，

∴DE＝BD﹣BE＝5﹣＝；

（3）证明：∵∠CAD＝60°，

∴∠CBD=60°，∠ACD=∠ABD，

∵DC＝DE，

∴∠ACD=∠DEC，

∵∠ABC+∠ADC=∠ABC+∠ABF=180°，

∴∠FBD=180°，

∴∠ABF＝∠ADC=120°

＝120°﹣∠ACD

＝120°﹣∠DEC

＝120°﹣（60°+∠ADE）

＝60°﹣∠ADE，

而∠F＝60°﹣∠ACF，

∵∠ACF＝∠ADE，

∴∠ABF＝∠F，

∴AB＝AF．

∵四边形ABCD内接于圆，

∴∠ABD＝∠ACD，

又∵DE＝DC，

∴∠DCE＝∠DEC＝∠AEB，

∴∠ABD＝∠AEB，

∴AB＝AE．

∴AE＝AF．