题目内容
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
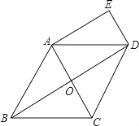
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)由DE∥AC和AE∥BD得到:四边形AODE是平行四边形,由菱形ABCD中AC和BD是对角线得到:AC⊥BD,综合以上两点可得平行四边形AODE是矩形;(2)由∠BCD=120°,AB∥CD得:∠ABC=180°﹣120°=60°,又因为AB=BC得:△ABC是等边三角形,所以OA=![]() ×4=2,在菱形ABCD中,AC⊥BD,由勾股定理OB=
×4=2,在菱形ABCD中,AC⊥BD,由勾股定理OB=![]() ,由四边形ABCD是菱形得:OD=OB=
,由四边形ABCD是菱形得:OD=OB=![]() ,所以四边形AODE的面积=OAOD=2
,所以四边形AODE的面积=OAOD=2![]() (或
(或![]() );
);
试题解析:
(1)∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是矩形,
故,四边形AODE是矩形;
(2)∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=![]() ×4=2,
×4=2,
∵在菱形ABCD中,AC⊥BD
∴由勾股定理OB=![]()
∵四边形ABCD是菱形,
∴OD=OB=![]() ,
,
∴四边形AODE的面积=OAOD=2![]() (或
(或![]() )
)

练习册系列答案
相关题目


