题目内容
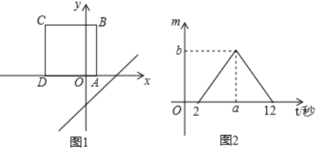
【题目】如图,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
①当t=![]() 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;
②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
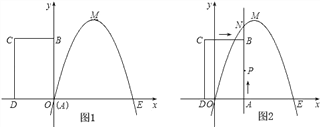
【答案】(1) y=﹣x2+4x;(2) ①点P不在直线ME上,理由见解析;②S存在最大值,理由见解析.
【解析】分析:(1)设出抛物线的顶点式y=a(x-2)2+4,将原点的坐标代入解析式就可以求出a的值,从而求出函数的解析式.
(2)①由(1)中抛物线的解析式可以求出E点的坐标,从而可以求出ME的解析式,再将P点的坐标代入直线的解析式就可以判断P点是否在直线ME上.
②设出点N(t,-(t-2)2+4),可以表示出PN的值,根据梯形的面积公式可以表示出S与t的函数关系式,从而可以求出结论.
详解:(1)因所求抛物线的顶点M的坐标为(2,4),
故可设其关系式为y=a(x﹣2)2+4
又∵抛物线经过O(0,0),
∴得a(0﹣2)2+4=0,
解得a=﹣1
∴所求函数关系式为y=﹣(x﹣2)2+4,
即y=﹣x2+4x.
(2)①点P不在直线ME上.
根据抛物线的对称性可知E点的坐标为(4,0),
又M的坐标为(2,4),
设直线ME的关系式为y=kx+b.
于是得![]() ,
,
解得![]()
所以直线ME的关系式为y=﹣2x+8.
由已知条件易得,当t=![]() 时,OA=AP=
时,OA=AP=![]() ,
,
∴P(![]() ,
,![]() )
)
∵P点的坐标不满足直线ME的关系式y=﹣2x+8.
∴当t=![]() 时,点P不在直线ME上.
时,点P不在直线ME上.
②S存在最大值.理由如下:
∵点A在x轴的非负半轴上,且N在抛物线上,
∴OA=AP=t.
∴点P,N的坐标分别为(t,t)、(t,﹣t2+4t)
∴AN=﹣t2+4t(0≤t≤3),
∴AN﹣AP=(﹣t2+4t)﹣t=﹣t2+3t=t(3﹣t)≥0,
∴PN=﹣t2+3t
(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD,
∴S=![]() DCAD=
DCAD=![]() ×3×2=3.
×3×2=3.
(ⅱ)当PN≠0时,以点P,N,C,D为顶点的多边形是四边形
∵PN∥CD,AD⊥CD,
∴S=![]() (CD+PN)AD=
(CD+PN)AD=![]() [3+(﹣t2+3t)]×2=﹣t2+3t+3=﹣(t﹣
[3+(﹣t2+3t)]×2=﹣t2+3t+3=﹣(t﹣![]() )2+
)2+![]()
其中(0<t<3),由a=﹣1,0<![]() <3,此时S最大=
<3,此时S最大=![]() .
.
综上所述,当t=![]() 时,以点P,N,C,D为顶点的多边形面积有最大值,这个最大值为
时,以点P,N,C,D为顶点的多边形面积有最大值,这个最大值为![]() .
.
说明:(ⅱ)中的关系式,当t=0和t=3时也适合.

 阅读快车系列答案
阅读快车系列答案