题目内容

已知：如图，点P是正方形ABCD内的一点，连结PA，PB，PC．

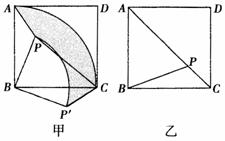
（1）如图甲，将△PAB绕点B顺时针旋转90°到△的位置．

①设AB的长为a，PB的长为b(b<a)，求△PAB旋转到△的过程中边PA所扫过区域（图甲中阴影部分）的面积；

②若PA＝3，PB＝6，∠APB＝135°，求PC的长．

（2）如图乙，若PA²＋PC²＝2PB²，请说明点P必在对角线AC上．

(1)①②连结PP′，证△为等腰直角三角形，从而PC＝9．

(2)将△PAB绕点B顺时针旋转90°到△P′CB的位置，由勾股逆定理证出∠＝90°，再证∠BPC＋∠APB＝180°，即点P在对角线AC上．

说明：（1）6分，（2）4分.

练习册系列答案

原创讲练测课优新突破系列答案

学优冲刺100系列答案

名校秘题小学毕业升学系统总复习系列答案

名师面对面小考满分策略系列答案

教材全解字词句篇系列答案

课时练全优达标测试卷系列答案

万唯中考试题研究系列答案

1课3练世界图书出版公司系列答案

学生用书系列答案

全优训练系列答案

相关题目

已知：如图，点O是平面直角坐标系的原点，点A的坐标为（0，-4），点B为x轴上一动点，以线段AB为边作正方形ABCD（按逆时针方向标记），正方形ABCD随着点B的运动而随之相应变动．点E为y轴的正半轴与正方形A

BCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
（1）当t=3时，求点C的坐标；
（2）当t＞0时，求m与t之间的函数关系式；
（3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

（2012•房山区一模）已知：如图，点P是线段AB上的动点，分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD，AD和BC交于点M．
（1）当△APC和△BPD面积之和最小时，直接写出AP：PB的值和∠AMC的度数；
（2）将点P在线段AB上随意固定，再把△BPD按顺时针方向绕点P旋转一个角度α，当α＜60°时，旋转过程中，∠AMC的度数是否发生变化？证明你的结论．
（3）在第（2）小题给出的旋转过程中，若限定60°＜α＜120°，∠AMC的大小是否会发生变化？若变化，请写出∠AMC的度数变化范围；若不变化，请写出∠AMC的度数．

已知：如图，点P是线段AB上的动点，分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD，AD和BC交于点M．
（1）当△APC和△BPD面积之和最小时，直接写出AP：PB的值和∠AMC的度数；
（2）将点P在线段AB上随意固定，再把△BPD按顺时针方向绕点P旋转一个角度α，当α＜60°时，旋转过程中，∠AMC的度数是否发生变化？证明你的结论．
（3）在第（2）小题给出的旋转过程中，若限定60°＜α＜120°，∠AMC的大小是否会发生变化？若变化，请写出∠AMC的度数变化范围；若不变化，请写出∠AMC的度数．

已知：如图，点O是平面直角坐标系的原点，点A的坐标为（0，-4），点B为x轴上一动点，以线段AB为边作正方形ABCD（按逆时针方向标记），正方形ABCD随着点B的运动而随之相应变动．点E为y轴的正半轴与正方形ABCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
（1）当t=3时，求点C的坐标；
（2）当t＞0时，求m与t之间的函数关系式；
（3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

（2013•惠山区一模）已知：如图，点O是平面直角坐标系的原点，点A的坐标为（0，-4），点B为x轴上一动点，以线段AB为边作正方形ABCD（按逆时针方向标记），正方形ABCD随着点B的运动而随之相应变动．点E为y轴的正半轴与正方形ABCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
（1）当t=3时，求点C的坐标；
（2）当t＞0时，求m与t之间的函数关系式；
（3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．