题目内容
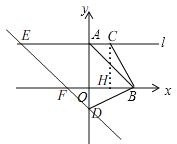
【题目】如图,在平面直角坐标系中,O是坐标原点,点A、B分别在y轴的正半轴和x轴的正半轴上,OA=OB,△AOB的面积为18.过点A作直线l⊥y轴.
(1)求点A的坐标;
(2)点C是第一象限直线l上一动点,连接BC,过点B作BD⊥BC,交y轴于点设点D的纵坐标为t,点C的横坐标为d,求t与d的关系式;
(3)在(2)的条件下,过点D作直线DF∥AB,交x轴于点F,交直线l于点E,OF=![]() EC时,求点E的坐标.
EC时,求点E的坐标.

【答案】(1)A(0,6);(2)d-t=6;(3)(-8,6)或(-4,6).
【解析】
(1)根据三角形的面积求出OA,即可得出结论;
(2)分三种情况:①当0<d<6时,构造出全等三角形,判断出BH=OD,即可得出结论;
②当d>6时,同①的方法即可得出结论;
③当d=6时,t=0,即可得出结论;
(3)①当0<d<6时,判断出OF=OD=-t,同理:AE6-t,CE=6-t+d,用OF=![]() EC,建立方程,联立(2)的方程即可得出结论;
EC,建立方程,联立(2)的方程即可得出结论;
②当d>6时,同①的方法即可得出结论;
③当d=6时,点D和点O重合,判断出点E不存在.
(1)∵△AOB的面积为18,![]() OAOB=18,
OAOB=18,
∵OA=OB,
∴OA2=36,
∴OA=6,
∴A(0,6);
(2)①当0<d<6时,如图,过点C作CH⊥x轴于H,
∴∠BCH+∠CBH=90°,
∵∠CBD=90°,
∴∠CBH+∠DBO=90°,
∴∠BCH=∠DBO,
∵AC∥x轴,
∴CH=OA,
∵OA=OB,
∴CH=OB,
∴△BCH≌△DBO(AAS),
∴BH=OD,
由(1)知,OB=OA=6,
∵C的横坐标为d,
∴BH=6-d,
∴OD=6-d,
∴6-d=-t,
∴d-t=6,
②当d>6时,同①的方法得,d-t=6,
③当d=6时,t=0,
∴d-t=6,即:t与d的关系式为d-t=6;
(3)①当0<d<6时,如图,

∵OA=OB,
∴∠ABO=45°,
∵EF∥AB,
∴∠EFG=45°,
∴∠OFD=45°,
∴∠ODF=45°=∠ODF,
∴OF=OD=-t,
同理:AE=AD=6-t,
∴CE=AE+AC=6-t+d,
∵OF=![]() EC,
EC,
∴6-t+d=6×(-t),
∴5t+d+6=0,
由(2)知,d-t=6,
∴t=-2,d=4
∴AE=8,
∴E(-8,6),
②当d>6时,同①的方法得,E(-4,6),
③当d=6时,点E不存在,
即:满足条件的点E的坐标为(-8,6)或(-4,6).

 特高级教师点拨系列答案
特高级教师点拨系列答案