题目内容
(2013•江宁区二模)如图1,在平面直角坐标系中,二次函数y=-x2-2x+2的图象与y轴交于点C,以OC为一边向左侧作正方形OCBA.
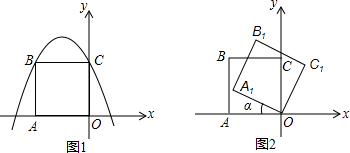
(1)判断点B是否在二次函数y=-x2-2x+2的图象上?并说明理由;
(2)用配方法求二次函数y=-x2-2x+2的图象的对称轴;
(3)如图2,把正方形OCBA绕点O顺时针旋转α后得到正方形A1B1C1O(0°<α<90°).
①当tanα﹦
时,二次函数y=-x2-2x+2的图象的对称轴上是否存在一点P,使△PB1C1为直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由.
②在二次函数y=-x2-2x+2的图象的对称轴上是否存在一点P,使△PB1C1为等腰直角三角形?若存在,请直接写出此时tanα的值;若不存在,请说明理由﹒
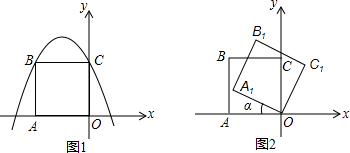
(1)判断点B是否在二次函数y=-x2-2x+2的图象上?并说明理由;
(2)用配方法求二次函数y=-x2-2x+2的图象的对称轴;
(3)如图2,把正方形OCBA绕点O顺时针旋转α后得到正方形A1B1C1O(0°<α<90°).
①当tanα﹦
| 1 | 2 |
②在二次函数y=-x2-2x+2的图象的对称轴上是否存在一点P,使△PB1C1为等腰直角三角形?若存在,请直接写出此时tanα的值;若不存在,请说明理由﹒
分析:(1)令x=0,求出y的值,得到正方形ABCO的边长,然后写出点B的坐标,再把横坐标代入二次函数关系式,计算即可验证;
(2)根据配方法,先提取-1,然后整理成完全平方公式的形式得到顶点式解析式,再写出对称轴即可;
(3)①设旋转后的正方形OA1B1C1的边B1C1交y轴于点D,二次函数y=-x2-2x+2的图象的对称轴交OA1于点E,交x轴于点F,然后分(i)点B1为直角顶点时,根据tanα=
求出EF,再利用勾股定理列式求出OE,然后求出A1E,再根据Rt△EFO和Rt△EA1P1相似,利用相似三角形对应边成比例列式求出P1E,然后求出P1F,即可得到点P的坐标;(ii)点C1为直角顶点时,根据同角的余角相等求出∠P3=∠EOF,再根据正切值求出P3F,即可得到点P的坐标;(iii)B1C1为斜边时,以B1C1为直径的圆与对称轴的交点即为所求,求出∠AOA1=∠C1OD,再根据α的正切值求出C1D=1,得到点D是B1C1的中点,再求出以B1C1为直径的圆与对称轴的交点只有一个P2,然后利用勾股定理列式求出OD的长,即可得到点P的坐标;
②根据正方形的性质,点A1落在对称轴上时,点A1即为所求的点P,利用勾股定理求出P1F,然后根据锐角的正切的定义写出即可;点P为A1B1的延长线与对称轴的交点时,由Rt△P2A1E和Rt△OFE相似,利用相似三角形对应边成比例求出A1E=4EF,设再用EF表示出OE,在Rt△OEF中,利用勾股定理列出方程求出EF的长,再根据锐角的正切的定义列式即可得解.
(2)根据配方法,先提取-1,然后整理成完全平方公式的形式得到顶点式解析式,再写出对称轴即可;
(3)①设旋转后的正方形OA1B1C1的边B1C1交y轴于点D,二次函数y=-x2-2x+2的图象的对称轴交OA1于点E,交x轴于点F,然后分(i)点B1为直角顶点时,根据tanα=
| 1 |
| 2 |
②根据正方形的性质,点A1落在对称轴上时,点A1即为所求的点P,利用勾股定理求出P1F,然后根据锐角的正切的定义写出即可;点P为A1B1的延长线与对称轴的交点时,由Rt△P2A1E和Rt△OFE相似,利用相似三角形对应边成比例求出A1E=4EF,设再用EF表示出OE,在Rt△OEF中,利用勾股定理列出方程求出EF的长,再根据锐角的正切的定义列式即可得解.
解答:解:(1)令x=0,y=2,
∴正方形的边长为2,
∴由题意得点B的坐标为(-2,2),
把x=-2代入二次函数关系式y=-x2-2x+2中,得y=2,
所以点B在二次函数y=-x2-2x+2的图象上;
(2)y=-x2-2x+2=-(x2+2x-2)=-(x+1)2+3,
所以,二次函数y=-x2-2x+2的图象的对称轴直线x=-1;
(3)①存在.
设旋转后的正方形OA1B1C1的边B1C1交y轴于点D,
二次函数y=-x2-2x+2的图象的对称轴交OA1于点E,交x轴于点F,
(i)当点B1为直角顶点,显然A1B1与对称轴的交点P1即为所求,
∵tanα=
=
=
,
∴EF=
,
根据勾股定理,OE=
=
=
,
∴A1E=2-
,
由Rt△EFO∽Rt△EA1P1,可得
=
,
即
=
,
解得P1E=2
-
,
∴P1F=2
-
+
=2
-2,
因此,P1点坐标为(-1,2
-2);
(ii)当点C1为直角顶点,显然射线C1O与对称轴的交点P3即为所求,
∵∠EOF+∠FOP3=90°,∠FOP3+∠P3=90°,
∴∠P3=∠EOF=α,
tan∠P3=tanα=
=
=
,
解得P3F=2,
因此,P3点的坐标为(-1,-2);
(iii)当B1C1为斜边时,以B1C1为直径的圆与对称轴的交点即为所求,
由已知,∵∠AOA1=∠C1OD,
∴tanα﹦
=
,
∴C1D=
OC1=1,即点D是B1C1的中点,
∵B1C1的中点D到对称轴的距离恰好等于1,
∴以B1C1为直径的圆与对称轴的交点只有一个P2,
根据勾股定理,OD=
=
=
,
因此,P2点的坐标为(-1,
),
故满足题设条件的P点有三个:P1(-1,2
-2),P2(-1,
),P3(-1,-2);

②存在.
如图1,点A1落在对称轴上时,根据勾股定理,P1F=
=
,
tanα=
=
=
;
如图2,点P为A1B1的延长线与对称轴的交点时,
∵△PB1C1为等腰直角三角形,
∴P2B1=B1C1=2,
∴A1P2=2+2=4,
易得,Rt△P2A1E∽Rt△OFE,
∴
=
,
即
=
,
∴A1E=4EF,
∴OE=2-4EF,
在Rt△OEF中,OF2+EF2=OE2,
即12+EF2=(2-4EF)2,
整理得,15EF2-16EF+3=0,
解得EF=
或EF=
(舍去),
所以,tanα=
=
=
.
∴正方形的边长为2,
∴由题意得点B的坐标为(-2,2),
把x=-2代入二次函数关系式y=-x2-2x+2中,得y=2,
所以点B在二次函数y=-x2-2x+2的图象上;
(2)y=-x2-2x+2=-(x2+2x-2)=-(x+1)2+3,
所以,二次函数y=-x2-2x+2的图象的对称轴直线x=-1;
(3)①存在.
设旋转后的正方形OA1B1C1的边B1C1交y轴于点D,
二次函数y=-x2-2x+2的图象的对称轴交OA1于点E,交x轴于点F,
(i)当点B1为直角顶点,显然A1B1与对称轴的交点P1即为所求,
∵tanα=
| EF |
| OF |
| EF |
| 1 |
| 1 |
| 2 |
∴EF=
| 1 |
| 2 |
根据勾股定理,OE=
| EF2+OF2 |
(
|
| ||
| 2 |
∴A1E=2-
| ||
| 2 |
由Rt△EFO∽Rt△EA1P1,可得
| A1E |
| EF |
| P1E |
| OE |
即
2-
| ||||
|
| P1E | ||||
|
解得P1E=2
| 5 |
| 5 |
| 2 |
∴P1F=2
| 5 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
因此,P1点坐标为(-1,2
| 5 |
(ii)当点C1为直角顶点,显然射线C1O与对称轴的交点P3即为所求,
∵∠EOF+∠FOP3=90°,∠FOP3+∠P3=90°,
∴∠P3=∠EOF=α,
tan∠P3=tanα=
| OF |
| P3F |
| 1 |
| P3F |
| 1 |
| 2 |
解得P3F=2,
因此,P3点的坐标为(-1,-2);
(iii)当B1C1为斜边时,以B1C1为直径的圆与对称轴的交点即为所求,
由已知,∵∠AOA1=∠C1OD,
∴tanα﹦
| C1D |
| OC1 |
| 1 |
| 2 |
∴C1D=
| 1 |
| 2 |
∵B1C1的中点D到对称轴的距离恰好等于1,
∴以B1C1为直径的圆与对称轴的交点只有一个P2,
根据勾股定理,OD=
| OC12+C1D2 |
| 22+12 |
| 5 |
因此,P2点的坐标为(-1,
| 5 |
故满足题设条件的P点有三个:P1(-1,2
| 5 |
| 5 |

②存在.
如图1,点A1落在对称轴上时,根据勾股定理,P1F=
| 22-12 |
| 3 |
tanα=
| P1F |
| OF |
| ||
| 1 |
| 3 |
如图2,点P为A1B1的延长线与对称轴的交点时,
∵△PB1C1为等腰直角三角形,
∴P2B1=B1C1=2,
∴A1P2=2+2=4,
易得,Rt△P2A1E∽Rt△OFE,
∴
| A1P2 |
| OF |
| A1E |
| EF |
即
| 4 |
| 1 |
| A1E |
| EF |
∴A1E=4EF,
∴OE=2-4EF,
在Rt△OEF中,OF2+EF2=OE2,
即12+EF2=(2-4EF)2,
整理得,15EF2-16EF+3=0,
解得EF=
8-
| ||
| 15 |
8+
| ||
| 15 |
所以,tanα=
| EF |
| OF |
| EF |
| 1 |
8-
| ||
| 15 |
点评:本题是二次函数综合题型,主要考查了求二次函数图象与坐标轴的交点,正方形的性质,配方法,相似三角形的判定与性质,锐角三角函数,等腰直角三角形的性质,难点在于第(3)小题的两个小题都要分情况讨论,并且运算量较大.

练习册系列答案
相关题目
 (2013•江宁区二模)甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
(2013•江宁区二模)甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( ) (2013•江宁区二模)如图,若将木条a绕点O旋转后与木条b平行,则旋转角的最小值为
(2013•江宁区二模)如图,若将木条a绕点O旋转后与木条b平行,则旋转角的最小值为 (2013•江宁区二模)在如图所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),将△ABC绕点A逆时针旋转90°,则在△ABC扫过的区域中(不含边界上的点),到点O的距离为无理数的格点的个数是( )
(2013•江宁区二模)在如图所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),将△ABC绕点A逆时针旋转90°,则在△ABC扫过的区域中(不含边界上的点),到点O的距离为无理数的格点的个数是( )