题目内容
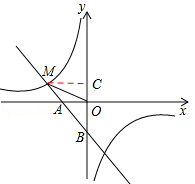
如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数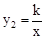 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;(2)求点B到直线OM的距离.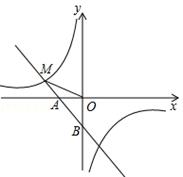
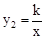 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).(1)求反比例函数的解析式;(2)求点B到直线OM的距离.

(1)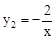 (2)
(2)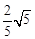
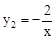 (2)
(2)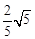
解:(1)∵一次函数y1=﹣x﹣1过M(﹣2,m),∴m=1。∴M(﹣2,1)。
把M(﹣2,1)代入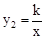 得:k=﹣2。
得:k=﹣2。
∴反比列函数为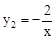 。
。
(2)设点B到直线OM的距离为h,过M点作MC⊥y轴,垂足为C。
∵一次函数y1=﹣x﹣1与y轴交于点B,
∴点B的坐标是(0,﹣1)。
∴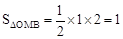 。
。
在Rt△OMC中,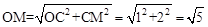 ,
,
∵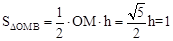 ,∴
,∴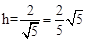 。
。
∴点B到直线OM的距离为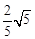 .
.
(1)根据一次函数解析式求出M点的坐标,再把M点的坐标代入反比例函数解析式即可。
(2)设点B到直线OM的距离为h,过M点作MC⊥y轴,垂足为C,根据一次函数解析式表示出B点坐标,利用△OMB的面积=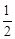 ×BO×MC算出面积,利用勾股定理算出MO的长,再次利用三角形的面积公式可得
×BO×MC算出面积,利用勾股定理算出MO的长,再次利用三角形的面积公式可得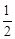 OM•h,根据前面算的三角形面积可算出h的值
OM•h,根据前面算的三角形面积可算出h的值
把M(﹣2,1)代入
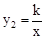 得:k=﹣2。
得:k=﹣2。∴反比列函数为
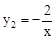 。
。(2)设点B到直线OM的距离为h,过M点作MC⊥y轴,垂足为C。

∵一次函数y1=﹣x﹣1与y轴交于点B,
∴点B的坐标是(0,﹣1)。
∴
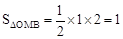 。
。在Rt△OMC中,
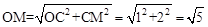 ,
,∵
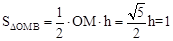 ,∴
,∴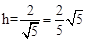 。
。∴点B到直线OM的距离为
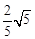 .
.(1)根据一次函数解析式求出M点的坐标,再把M点的坐标代入反比例函数解析式即可。
(2)设点B到直线OM的距离为h,过M点作MC⊥y轴,垂足为C,根据一次函数解析式表示出B点坐标,利用△OMB的面积=
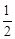 ×BO×MC算出面积,利用勾股定理算出MO的长,再次利用三角形的面积公式可得
×BO×MC算出面积,利用勾股定理算出MO的长,再次利用三角形的面积公式可得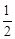 OM•h,根据前面算的三角形面积可算出h的值
OM•h,根据前面算的三角形面积可算出h的值
练习册系列答案
相关题目
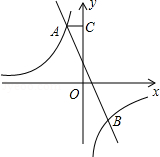
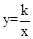 和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=
和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=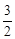 .
.
 的图象上有两点(-1,y1),
的图象上有两点(-1,y1), ,则y1-y2的值是【 】
,则y1-y2的值是【 】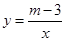 的图像在
的图像在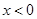 的范围内,
的范围内,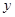 随
随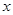 的增大而减小,那么
的增大而减小,那么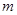 取值范是 .
取值范是 .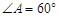 ,点M从点A出发,以1㎝/s的速度向点B运动,点N从点A 同时出发,以2㎝/s的速度经过点D向点C运动,当其中一个动点到达端点时,另一个动点也随之停止运动. 则△AMN的面积
,点M从点A出发,以1㎝/s的速度向点B运动,点N从点A 同时出发,以2㎝/s的速度经过点D向点C运动,当其中一个动点到达端点时,另一个动点也随之停止运动. 则△AMN的面积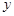 (㎝2) 与点M运动的时间
(㎝2) 与点M运动的时间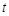 (s)的函数的图像大致是( )
(s)的函数的图像大致是( )
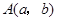 ,
,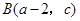 两点均在函数
两点均在函数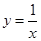 的图象上,且
的图象上,且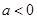 ,则
,则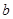 与
与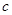 的大小关系为
的大小关系为
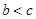

 的图象没有交点,则实数k的取值范围在数轴上表示为【 】。
的图象没有交点,则实数k的取值范围在数轴上表示为【 】。
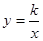 与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3……An的坐标是连续整数,分别过A1、A2……An作x轴的平行线于双曲线
与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3……An的坐标是连续整数,分别过A1、A2……An作x轴的平行线于双曲线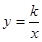 (x>0)及直线x=k分别交于点B1、B2,……Bn,C1、C2,……Cn.
(x>0)及直线x=k分别交于点B1、B2,……Bn,C1、C2,……Cn.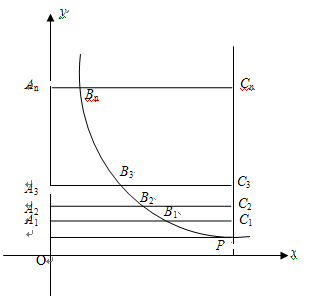
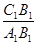 及
及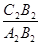 的值;
的值;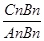 的值(直接写答案).
的值(直接写答案).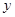 cm与宽
cm与宽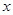 cm之间的函数关系用图象表示大致是
cm之间的函数关系用图象表示大致是 