题目内容
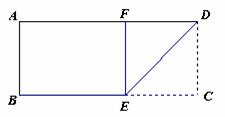
如图是一张矩形纸片ABCD，AD=6cm，若将纸片沿DE折叠，使DC落在DA上，点C的对应点为点F，若BE=2cm，则DE=（ ）A、2
| ||
| B、4cm | ||
C、4
| ||
| D、6cm |
分析：根据已知，得CE=4，从而根据勾股定理即可求得DE的长．
解答：解：∵AD=6cm，BE=2cm，
∴CE=4cm．
∴CD=CE=4cm．
根据勾股定理，得
DE=4
cm．
故选C．
∴CE=4cm．
∴CD=CE=4cm．
根据勾股定理，得
DE=4
| 2 |
故选C．
点评：此题主要是运用了折叠的性质和勾股定理．
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
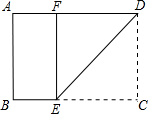
3、如图是一张矩形纸片ABCD，AD=10cm，若将纸片沿DE折叠，使DC落在DA上，点C的对应点为点F，若BE=6cm，则CD=（ ）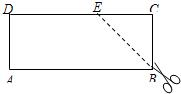
10、如图是一张矩形纸片ABCD，AB=10，AD=4，若用剪刀沿∠ABC的角平分线BE剪下，则DE的长等于（ ）
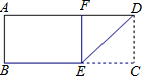如图是一张矩形纸片ABCD，AD=10cm，若将纸片沿DE折叠，使DC落在DA上，点C的对应点为点F，若BE=6cm，则CD=
，
，若将纸片沿
折叠，使
落在
上，
点
的对应点为点
，若
，则
（ ）
B．
C．
D．
