题目内容
(2012•和平区二模)已知抛物线y1=a(x-2)2-4(a≠0)经过点(0,-3),顶点为M,将抛物线y1向上平移b个单位可使平移后得到的抛物线y2经过坐标原点,抛物线y2的顶点为A,与x轴的另一个交点为B.
(1)求a的值;
(2)①b=
(3)①点P是y轴上一点,当|PA-PB|的值最大时,求点P的坐标;
②点E是x轴上一点,在抛物线y2上是否存在点F,使O(原点)、M、E、F四点构成以OM为一边的平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.

(1)求a的值;
(2)①b=
3
3
,②抛物线y2的函数表达式是y2=
(x-2)2-1
| 1 |
| 4 |
y2=
(x-2)2-1
;| 1 |
| 4 |
(3)①点P是y轴上一点,当|PA-PB|的值最大时,求点P的坐标;
②点E是x轴上一点,在抛物线y2上是否存在点F,使O(原点)、M、E、F四点构成以OM为一边的平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
分析:(1)将(0,-3)代入y1=a(x-2)2-4(a≠0)中,即可求得a的值.
(2)抛物线y1经过(0,-3),向上平移后经过原点即可(0,0),因此抛物线向上平移了3个单位,根据“上加下减”的平移规律即可得出y2的函数表达式.
(3)①当P、A、B三点不在同一直线上时,能构成△PAB,由三角形三边关系定理不难看出|PA-PB|<AB;若P、A、B三点共线时,|PA-PB|=AB,显然当|PA-PB|的值最大时,P、A、B三点共线,所以直接求出直线AB的解析式,该直线与y轴的交点即为符合条件的P点;
②点O、M已经确定了具体坐标,且OM是平行四边形的边,所以只考虑另一边EF即可,由于点E在x轴上,且OM
EF,所以可分两种情况讨论:
Ⅰ、点F在x轴下方,此时MF必与OB平行,即MF平行于x轴,此时M、F两点的纵坐标相同,由题意(y2由y1向上平移所得)可知,点F不可能在y2上,这种情况不成立;
Ⅱ、点F在x轴下方,由于平行四边形是中心对称图形,那么此时M、F的纵坐标互为相反数,可据此确定点F的坐标.
(2)抛物线y1经过(0,-3),向上平移后经过原点即可(0,0),因此抛物线向上平移了3个单位,根据“上加下减”的平移规律即可得出y2的函数表达式.
(3)①当P、A、B三点不在同一直线上时,能构成△PAB,由三角形三边关系定理不难看出|PA-PB|<AB;若P、A、B三点共线时,|PA-PB|=AB,显然当|PA-PB|的值最大时,P、A、B三点共线,所以直接求出直线AB的解析式,该直线与y轴的交点即为符合条件的P点;
②点O、M已经确定了具体坐标,且OM是平行四边形的边,所以只考虑另一边EF即可,由于点E在x轴上,且OM
| ∥ |
. |
Ⅰ、点F在x轴下方,此时MF必与OB平行,即MF平行于x轴,此时M、F两点的纵坐标相同,由题意(y2由y1向上平移所得)可知,点F不可能在y2上,这种情况不成立;
Ⅱ、点F在x轴下方,由于平行四边形是中心对称图形,那么此时M、F的纵坐标互为相反数,可据此确定点F的坐标.
解答:解:(1)抛物线y1=a(x-2)2-4(a≠0)经过点(0,-3),可得:
-3=a(0-2)2-4,
解得:a=
.
(2)∵经过(0,-3)的抛物线y1向上平移,经过(0,0)得到抛物线y2,
∴向上平移了3个单位,即b=3;
故抛物线y2:y2=
(x-2)2-4+3=
(x-2)2-1.
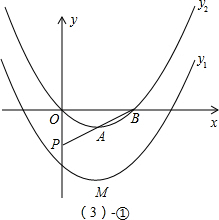 (3)①∵|PA-PB|≤AB,且当且仅当P、A、B共线时取等号,
(3)①∵|PA-PB|≤AB,且当且仅当P、A、B共线时取等号,
∴|PA-PB|的值最大时,P、A、B共线;
由(2)的抛物线解析式知:A(2,-1)、B(4,0),设直线AB的解析式:y=kx+b,有:
,
解得
故直线AB:y=
x-2,则P(0,-2).
②易知M(2,-4),分两种情况讨论:
Ⅰ、点F在x轴下方时,由于OM是平行四边形的边,则MF∥x轴,即F点的纵坐标为-4,显然点F不可能在抛物线y2上,此种情况不成立;
Ⅱ、点F在x轴上方时,由于平行四边形是中心对称图形,所以F点的纵坐标为4;
当y2=4时,
(x-2)2-1=4,解得:x=2±2
则F(2-2
,4)或(2+2
,4);
综上,存在符合条件的F点,且坐标为(2-2
,4)或(2+2
,4).
-3=a(0-2)2-4,
解得:a=
| 1 |
| 4 |
(2)∵经过(0,-3)的抛物线y1向上平移,经过(0,0)得到抛物线y2,
∴向上平移了3个单位,即b=3;
故抛物线y2:y2=
| 1 |
| 4 |
| 1 |
| 4 |
 (3)①∵|PA-PB|≤AB,且当且仅当P、A、B共线时取等号,
(3)①∵|PA-PB|≤AB,且当且仅当P、A、B共线时取等号,∴|PA-PB|的值最大时,P、A、B共线;
由(2)的抛物线解析式知:A(2,-1)、B(4,0),设直线AB的解析式:y=kx+b,有:
|
解得
|
故直线AB:y=
| 1 |
| 2 |
②易知M(2,-4),分两种情况讨论:
Ⅰ、点F在x轴下方时,由于OM是平行四边形的边,则MF∥x轴,即F点的纵坐标为-4,显然点F不可能在抛物线y2上,此种情况不成立;
Ⅱ、点F在x轴上方时,由于平行四边形是中心对称图形,所以F点的纵坐标为4;
当y2=4时,
| 1 |
| 4 |
| 5 |
则F(2-2
| 5 |
| 5 |
综上,存在符合条件的F点,且坐标为(2-2
| 5 |
| 5 |
点评:此题主要考查了二次函数解析式的确定、函数图象的平移规律、三角形三边关系定理以及平行四边形的判定等重要知识;(3)的难度较大,利用几何知识找出解题的思路是解题的关键,着重体现了数形结合的重要性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•和平区二模)如图,点P是菱形ABCD的对角线AC上一动点(不与点A、C重合).过点P且垂直于AC的直线交菱形ABCD的边于M、N两点.若AC=2,BD=1,设AP=x,S△AMN=y,则y关于x的函数图象的大致形状是( )
(2012•和平区二模)如图,点P是菱形ABCD的对角线AC上一动点(不与点A、C重合).过点P且垂直于AC的直线交菱形ABCD的边于M、N两点.若AC=2,BD=1,设AP=x,S△AMN=y,则y关于x的函数图象的大致形状是( ) (2012•和平区二模)如图,在直角坐标系中,O为坐标原点.已知反比例函数
(2012•和平区二模)如图,在直角坐标系中,O为坐标原点.已知反比例函数 (2012•和平区二模)如图,在Rt△ADC中,∠ADC=90°,以CD为直径的半圆O交AC于点E,点G是AD的中点.
(2012•和平区二模)如图,在Rt△ADC中,∠ADC=90°,以CD为直径的半圆O交AC于点E,点G是AD的中点.