题目内容
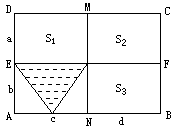
 在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF、MN将大长方形ABCD分成四个小长方形,已知DE=a,AE=b,AN=c,BN=d,且S1的面积为8,S2的面积为6,S3的面积为5,则阴影三角形的面积为________.
在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF、MN将大长方形ABCD分成四个小长方形,已知DE=a,AE=b,AN=c,BN=d,且S1的面积为8,S2的面积为6,S3的面积为5,则阴影三角形的面积为________.

分析:根据已知S1的面积为8,S2的面积为6,S3的面积为5,得出ac=8,ad=6,bd=5,求出c=
 d、b=
d、b=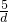 ,代入阴影三角形的面积
,代入阴影三角形的面积 cb求出即可.
cb求出即可.解答:∵S1的面积为8,S2的面积为6,S3的面积为5,
∴①S1=ac=8,②S2=ad=6,③S3=bd=5,
即①÷②得:
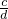 =
=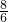 =
= ,
,c=
 d,
d,由③得:b=
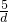 ,
,∵阴影三角形的面积是
 cb,
cb,∴阴影三角形的面积是:
 ×
× d×
d×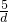 =
= .
.故答案为:
 .
.点评:本题考查了三角形的面积和矩形的性质的应用,关键是求出c=
 d和b=
d和b=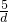 ,主要考查学生运用性质进行推理和计算的能力,题型较好,但有一定的难度.
,主要考查学生运用性质进行推理和计算的能力,题型较好,但有一定的难度. 
练习册系列答案
相关题目
 在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF、MN将大长方形ABCD分成四个小长方形,已知DE=a,AE=b,AN=c,BN=d,且S1的面积为8,S2的面积为6,S3的面积为5,则阴影三角形的面积为
在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF、MN将大长方形ABCD分成四个小长方形,已知DE=a,AE=b,AN=c,BN=d,且S1的面积为8,S2的面积为6,S3的面积为5,则阴影三角形的面积为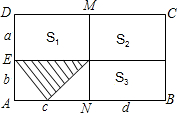 在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF、MN将大长方形ABCD分成四个小长方形,已知DE=a,AE=b,AN=c,BN=d,且S1的面积为8,S2的面积为6,S3的面积为5,则阴影三角形的面积为( )
在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF、MN将大长方形ABCD分成四个小长方形,已知DE=a,AE=b,AN=c,BN=d,且S1的面积为8,S2的面积为6,S3的面积为5,则阴影三角形的面积为( )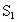 的面积为8,
的面积为8,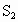 的面积为6,
的面积为6,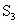 的面积为5,则阴影三角形的面积为________.
的面积为5,则阴影三角形的面积为________.