题目内容
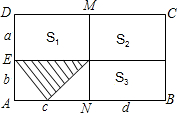 在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF、MN将大长方形ABCD分成四个小长方形,已知DE=a,AE=b,AN=c,BN=d,且S1的面积为8,S2的面积为6,S3的面积为5,则阴影三角形的面积为( )
在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF、MN将大长方形ABCD分成四个小长方形,已知DE=a,AE=b,AN=c,BN=d,且S1的面积为8,S2的面积为6,S3的面积为5,则阴影三角形的面积为( )A、
| ||
| B、3 | ||
| C、4 | ||
D、
|
分析:首先根据题意可知ac=8,ad=6,bd=5,根据后两式求出ab之间的关系,再求出bc的值,又知阴影三角形的面积为
bc,即可得到答案.
| 1 |
| 2 |
解答:解:根据题意:
DE=a,AE=b,AN=c,BN=d,
且S1的面积为8,S2的面积为6,S3的面积为5,
故知ac=8…①
ad=6…②
bd=5…③,
②÷③得:a=
b…④,
把④代入①可得bc=
,
∵阴影三角形的面积=
bc=
.
故选A.
DE=a,AE=b,AN=c,BN=d,
且S1的面积为8,S2的面积为6,S3的面积为5,
故知ac=8…①
ad=6…②
bd=5…③,
②÷③得:a=
| 6 |
| 5 |
把④代入①可得bc=
| 20 |
| 3 |
∵阴影三角形的面积=
| 1 |
| 2 |
| 10 |
| 3 |
故选A.
点评:本题主要考查面积即等积变换的知识点,解答本题的关键是求出bc的值,本题难度较大.

练习册系列答案
相关题目
 在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF、MN将大长方形ABCD分成四个小长方形,已知DE=a,AE=b,AN=c,BN=d,且S1的面积为8,S2的面积为6,S3的面积为5,则阴影三角形的面积为
在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF、MN将大长方形ABCD分成四个小长方形,已知DE=a,AE=b,AN=c,BN=d,且S1的面积为8,S2的面积为6,S3的面积为5,则阴影三角形的面积为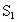 的面积为8,
的面积为8,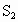 的面积为6,
的面积为6,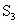 的面积为5,则阴影三角形的面积为________.
的面积为5,则阴影三角形的面积为________.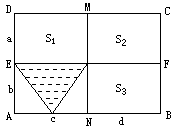
 在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF、MN将大长方形ABCD分成四个小长方形,已知DE=a,AE=b,AN=c,BN=d,且S1的面积为8,S2的面积为6,S3的面积为5,则阴影三角形的面积为________.
在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF、MN将大长方形ABCD分成四个小长方形,已知DE=a,AE=b,AN=c,BN=d,且S1的面积为8,S2的面积为6,S3的面积为5,则阴影三角形的面积为________.