Question

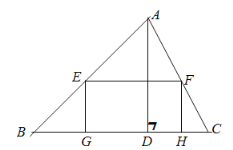
【题目】如图，AD是△ABC的高，点G、H在BC边上，点E在AB边上，点F在AC边上，BC=10cm，AD=8cm，四边形EFHG是矩形．

（1）△AEF与△ABC相似吗？请说明理由．

（2）若矩形EFHG的面积为15cm2，求这个矩形的长和宽．

Answer 1

【答案】（1）见解析；（2），2或6，．

【解析】

（1）根据EF∥BC，可得∠AEF=∠B，∠AFE=∠C，进而可证明相似；（2）设矩形EFHG的长为xcm，根据题意可得矩形EFHG的宽为cm，利用相似三角形的性质求出x的值即可.

（1）相似，理由如下：

∵四边形EFHG是矩形，

∴EF∥BC，

∴∠AEF=∠B，∠AFE=∠C，

∴△AEF∽△ABC；

（2）如图，记EF与AD的交点为K，

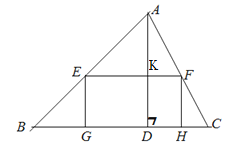
设矩形EFHG的长为xcm，

∵四边形EFHG是面积为15cm2的矩形，

∴矩形EFHG的宽为：cm，

∴EF=GH=xcm，EG=FH=cm，

∵AD是△ABC的高，四边形EFHG是矩形，

∴EF∥BC，KD=EG=cm，

∴AD⊥EF，AK=AD-KD=（8-）cm，

∵△AEF∽△ABC，

∴AK∶AD＝EF∶BC，

∴（8-）∶8＝x∶10，

∴4x2-40x+75=0，

∴（2x-15）（2x-5）=0，

解得：或，

当时，=2；

当时，=6．

∴这个矩形的长和宽为：，2或6，．