题目内容
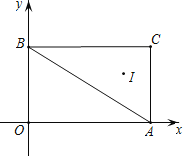
【题目】如图1,在平面直角坐标系![]() 中,已知点
中,已知点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针分别旋转
按顺时针分别旋转![]() ,
,![]() 得到
得到![]() ,
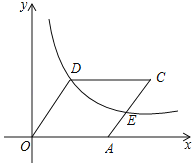
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ;抛物线
;抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() .
.

(1)点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________;抛物线
的坐标为________;抛物线![]() 的解析式为________,抛物线
的解析式为________,抛物线![]() 的解析式为________;
的解析式为________;
(2)如果点![]() 是直线
是直线![]() 上方抛物线
上方抛物线![]() 上的一个动点.
上的一个动点.
①若![]() ,求
,求![]() 点的坐标;
点的坐标;
②如图2,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,记
,记![]() ,求
,求![]() 与
与![]() 的函数关系式.当
的函数关系式.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ,
,![]() :
:![]() ,
,![]() :
:![]() .(2)①符合条件的点
.(2)①符合条件的点![]() 的坐标为
的坐标为![]() 或
或![]() .②
.②![]() .
.
【解析】
(1)根据旋转的性质,可得C,E,F的坐标,根据待定系数法求解析式;
(2)①根据P点关于直线CA或关于x轴对称直线与抛物线交点坐标,求出解析式,联立方程组求解;
②根据图象上的点满足函数解析式,可得P、N、M纵坐标,根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据x取值范围讨论h范围.
(1)由旋转可知,OC=6,OE=2,
则点C坐标为(-6,0),E点坐标为(2,0),
分别利用待定系数法求C1解析式为:y=-![]() x24x6,C2解析式为:y=-
x24x6,C2解析式为:y=-![]() x22x+6
x22x+6
(2)①若点P在x轴上方,∠PCA=∠ABO时,则CA1与抛物线C1的交点即为点P,如图,
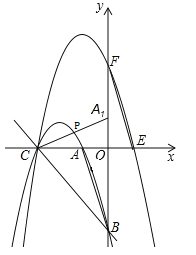
设直线CA1的解析式为:y=k1x+b1
∴![]()
解得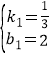
∴直线CA1的解析式为:y=![]() x+2
x+2
联立: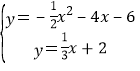 ,解得
,解得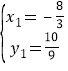 或
或![]() (舍去),
(舍去),
∴P(![]() )
)
若点P在x轴下方,∠PCA=∠ABO时,则CH与抛物线C1的交点即为点P,如图,
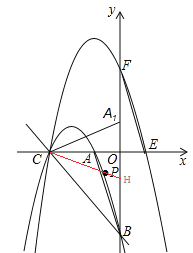
易知OH=OA,
∴H(0,-2)
设直线CH的解析式为:y=k2x+b2
∴![]()
解得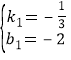
∴直线CH的解析式为:y=![]() x-2
x-2
联立: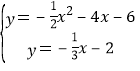 ,解得
,解得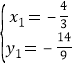 或
或![]() (舍去),
(舍去),
∴![]() ;
;
∴符合条件的点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
②设直线![]() 的解析式为:
的解析式为:![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,

设P(x,-![]() x24x6)
x24x6)
∴![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 的最大值为21.
的最大值为21.
∵![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .
.

 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案【题目】从2开始的连续偶数相加,它们和的情况如下表:
加数的个数(n) | 和(S) |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=12=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
… | … |
(1)根据表中的规律,直接写出2+4+6+8+10+12+14=________
(2)根据表中的规律猜想:S=2+4+6+8+…+2n=___________(用n的代数式表示);
(3)利用上题中的公式计算102+104+106+…+200的值(要求写出计算过程).
【题目】某校要从小红、小明和小亮三名同学中挑选一名同学参加数学素养大赛,在最近的四次专题测试中,他们三人的成绩如下表所示:
学生 专题 | 集合证明 | PISA问题 | 应用题 | 动点问题 |
小红 | 70 | 75 | 80 | 85 |
小明 | 80 | 80 | 72 | 76 |
小亮 | 75 | 75 | 90 | 65 |
(1)请算出小红的平均分为多少?
(2)该校根据四次专题考试成绩的重要程度不同而赋予每个专题成绩一个权重,权重比依次为x:1:2:1,最后得出三人的成绩(加权平均数),若从高分到低分排序为小亮、小明、小红,求正整数x的值.