题目内容
如图，将平行四边形ABCD折叠，使顶点D恰落在AB边上的点M处，折痕为AN，那么对于结论 ①MN∥BC，②MN=AM，下列说法正确的是
- A.①②都对
- B.①②都错
- C.①对②错
- D.①错②对
A
分析：根据题意，推出∠B=∠D=∠AMN，即可推出结论①，由AM=DA推出四边形AMND为菱形，因此推出②．
解答：∵平行四边形ABCD，
∴∠B=∠D=∠AMN，
∴MN∥BC，
∵AM=DA，
∴四边形AMND为菱形，
∴MN=AM．
故选A．
点评：本题主要考查翻折变换的性质、平行四边形的性质、菱形的判定和性质，平行线的判定，解题的关键在于熟练掌握有关的性质定理，推出四边形AMND为菱形．
分析：根据题意，推出∠B=∠D=∠AMN，即可推出结论①，由AM=DA推出四边形AMND为菱形，因此推出②．
解答：∵平行四边形ABCD，
∴∠B=∠D=∠AMN，
∴MN∥BC，
∵AM=DA，
∴四边形AMND为菱形，
∴MN=AM．
故选A．
点评：本题主要考查翻折变换的性质、平行四边形的性质、菱形的判定和性质，平行线的判定，解题的关键在于熟练掌握有关的性质定理，推出四边形AMND为菱形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14、如图，将平行四边形ABCD折叠，使顶点D恰落在AB边上的点M处，折痕为AN，那么对于结论 ①MN∥BC，②MN=AM，下列说法正确的是（ ）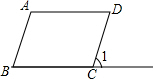
（2012•成都）如图，将平行四边形ABCD的一边BC延长至E，若∠A=110°，则∠1=
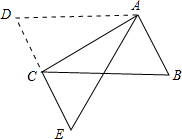（2013•德惠市二模）如图，将平行四边形纸片ABCD沿对角线AC折叠，点D落在点E处，AE恰好过BC边中点，若AB=3，BC=6，则∠B的大小为（ ）
如图，将平行四边形ABCD纸片沿EF折叠，使点C与点A重合，点D落在点G处．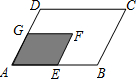
如图，将平行四边形AEFG变换到平行四边形ABCD，其中E，G分别是AB，AD的中点，下列叙述正确的有