题目内容
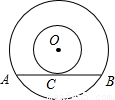
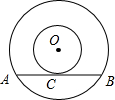已知两个同心圆：大圆的弦AB与小圆相切于点C，若AB=4cm，则由大圆和小圆所形成的圆环的面积为
- A.16πcm2
- B.2πcm2
- C.16cm2
- D.4πcm2
D
分析：连接OC、OA，构造出Rt△AOC，求出OA2-OC2的值，再乘以π即为环形的面积．
解答：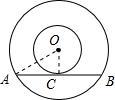
解：连接OC、OA，则OC⊥AB，
在Rt△AOC中，
OA2-OC2=AC2=（
）2=4，
所以环形的面积为OA2π-OC2π=4πcm2，
故选D．
点评：本题考查了切线的性质，勾股定理以及圆面积的计算公式．
分析：连接OC、OA，构造出Rt△AOC，求出OA2-OC2的值，再乘以π即为环形的面积．
解答：
解：连接OC、OA，则OC⊥AB，在Rt△AOC中，
OA2-OC2=AC2=（
）2=4，所以环形的面积为OA2π-OC2π=4πcm2，
故选D．
点评：本题考查了切线的性质，勾股定理以及圆面积的计算公式．
练习册系列答案
阅读快车系列答案
相关题目
已知两个同心圆：大圆的弦AB与小圆相切于点C，若AB=4cm，则由大圆和小圆所形成的圆环的面积为（ ）| A、16πcm2 | B、2πcm2 | C、16cm2 | D、4πcm2 |
