题目内容
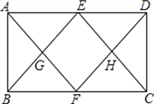
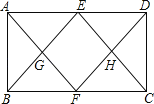
【题目】如图,在矩形ABCD中,E,F分别为AD,BC的中点,连结AF,DF,BE,CE,AF与BE交于G,DF与CE交于H.求证:四边形EGFH为菱形
【答案】证明见解析
【解析】试题分析: 根据一组对边平行且相等的四边形式平行四边形,可证明四边形AECF,BEDF是平行四边形,根据平行四边形的性质,可得GF与EH,EG与FH的关系,根据平行四边形的判定,可得EGFH的形状,根据三角形全等,可得EG与FG的关系,根据菱形的定义,可得证明结论.
试题解析:∵在矩形ABCD中AD=BC,且E,F分别是AD,BC的中点,
∴AE=DE=BF=CF,
又∵AD∥BC,
∴四边形AECF,BEDF是平行四边形,
∴GF∥EH,EG∥FH,
∴四边形EGFH是平行四边形,
在△AEG和△FBG中,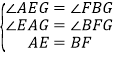 ,
,
∴△AEG≌△FBG(AAS),
∴EG=GB,AG=GF,
在△ABE和△BAF中,
∵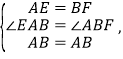
∴△ABE≌△BAF(SAS),
∴AF=BE,
∵EG=GB=![]() BE,AG=GF=
BE,AG=GF=![]() AF,
AF,
∴EG=GF,
∴四边形EGFH是菱形.

练习册系列答案
相关题目







