题目内容
若方程9x2-6（a+1）x+a2-3=0的两根之积等于1，则a的值是
- A.
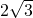
- B.
- C.
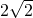
- D.
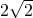
B
分析：先由判别式求出a的取值范围，再由两根之积求出a的值，不在取值范围内的值要舍去．
解答：∵△=36（a+1）2-4×9×（a2-3）
=36（2a+4）≥0
∴a≥-2．
∵x1•x2=
=1
∴a2=12
∴a1=2
，a2=-2（舍去）
故选B．
点评：本题考查的是一元二次方程根与系数的关系，由方程有两根求出a的取值范围，再由两根的积求出a的值，对不在取值范围内的值要舍去．
分析：先由判别式求出a的取值范围，再由两根之积求出a的值，不在取值范围内的值要舍去．
解答：∵△=36（a+1）2-4×9×（a2-3）
=36（2a+4）≥0
∴a≥-2．
∵x1•x2=
=1∴a2=12
∴a1=2
，a2=-2（舍去）故选B．
点评：本题考查的是一元二次方程根与系数的关系，由方程有两根求出a的取值范围，再由两根的积求出a的值，对不在取值范围内的值要舍去．
练习册系列答案
阅读快车系列答案
相关题目
; B.
; C.
; D.
.