题目内容
下列结论正确的是
①方程
=-2没有实数根；
②解方程（
）2-2（）=0时，若设y=，则原方程变形为y2-2y-3=0；
③存在这样的两个实数a、b，使得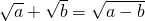
；
④当a≠0时，关于x的方程ax=b总有实数根．
- A.①②③
- B.①②④
- C.①③④
- D.②③④
C
分析：根据二次根式的意义、换元法、一元一次方程的解法分别分析各个选项．
解答：算术平方根应是非负数，故方程=-2没有实数根，①正确；
用换元法替换后，为y2-2y=0，②错误；
当b=0，a≥0时，式子成立，③正确；
当a≠0时，关于x的方程ax=b总有实数根，为x=
，④正确．
故选C．
点评：一个数的算术平方根一定是非负数，用换元法可使方程简化，当a≠0时，关于x的方程ax=b总有实数根，为x=．
分析：根据二次根式的意义、换元法、一元一次方程的解法分别分析各个选项．
解答：算术平方根应是非负数，故方程
=-2没有实数根，①正确；用换元法替换后，为y2-2y=0，②错误；
当b=0，a≥0时，式子成立，③正确；
当a≠0时，关于x的方程ax=b总有实数根，为x=
，④正确．故选C．
点评：一个数的算术平方根一定是非负数，用换元法可使方程简化，当a≠0时，关于x的方程ax=b总有实数根，为x=
． 
练习册系列答案
全能测控期末小状元系列答案
相关题目
已知两个样本--甲：2，4，6，8，10，乙：1，3，5，7，9．用S甲2和S乙2分别表示这两个样本的方差，则下列结论正确的是（ ）
| A、S甲2=S乙2 | B、S甲2＞S乙2 | C、S甲2＜S乙2 | D、无法确定 |
若样本x1+1，x2+1，…，xn+1的平均数为10，方差为2，则对于样本x1+2，x2+2，…，xn+2，下列结论正确的是（ ）
| A、平均数为10，方差为2 | B、平均数为11，方差为3 | C、平均数为11，方差为2 | D、平均数为12，方差为4 |
甲、乙两名选手在相同的条件下各射击6次，命中环数如下表，那么下列结论正确的是（ ）
| 甲 | 9 | 7 | 10 | 9 | 9 | 10 |
| 乙 | 10 | 8 | 9 | 8 | 10 | 9 |
A、甲的平均数是9，方差是
| ||
B、乙的平均数是9，方差是
| ||
| C、甲的平均数是8，方差是1 | ||
| D、乙的平均数是8，方差是1 |
6、一只小狗在如图的方砖上走来走去，最终停在阴影方砖上与空白方砖上的可能性相比较，下列结论正确的是（ ）