题目内容
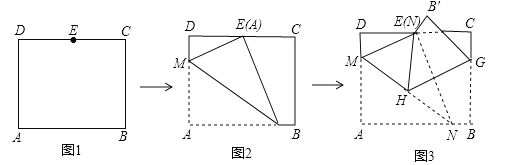
【题目】如图1,在矩形纸片ABCD中,AB=![]() ,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME/NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= .
,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME/NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= .
【答案】![]() .
.
【解析】
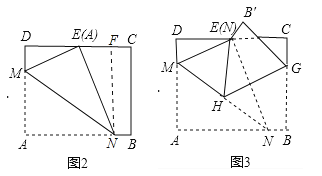
试题分析:如图2中,作NF⊥CD于F.设DM=x,则AM=EM=10﹣x,∵DE=EC,AB=CD=![]() ,∴DE=
,∴DE=![]() CD=
CD=![]() ,在RT△DEM中,∵
,在RT△DEM中,∵![]() ,∴
,∴![]() ,解得x=2.6,∴DM=2.6,AM=EM=7.4,∵∠DEN+∠NEF=90°,∠NEF+∠ENF=90°,∴∠DEM=∠ENF,∵∠D=∠EFN=90°,∴△DME∽△FEN,∴
,解得x=2.6,∴DM=2.6,AM=EM=7.4,∵∠DEN+∠NEF=90°,∠NEF+∠ENF=90°,∴∠DEM=∠ENF,∵∠D=∠EFN=90°,∴△DME∽△FEN,∴![]() ,∴
,∴![]() ,∴EN=
,∴EN=![]() ,∴AN=EN=
,∴AN=EN=![]() ,∴tan∠AMN=
,∴tan∠AMN=![]() =
=![]() ,如图3中,∵ME⊥EN,HG⊥EN,∴EM∥GH,∴∠NME=∠NHK,∵∠NME=∠AMN,∠EHG=∠NHK,∴∠AMN=∠EHG,∴tan∠EHG=tan∠AMN=
,如图3中,∵ME⊥EN,HG⊥EN,∴EM∥GH,∴∠NME=∠NHK,∵∠NME=∠AMN,∠EHG=∠NHK,∴∠AMN=∠EHG,∴tan∠EHG=tan∠AMN=![]() .故答案为:
.故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



