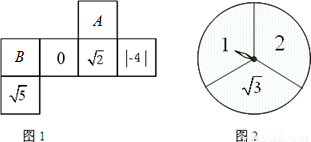题目内容
如图1是一个立方体的平面展开图，其中四个面上分别标有：0、| 2 |
| 5 |
| 3 |
（1）用树状图（或列表法）表示出两次自由转动转盘所有可能出现的结果；
（2）填入数值后，求立方体A、B两数的乘积大于A对面上的数的概率．
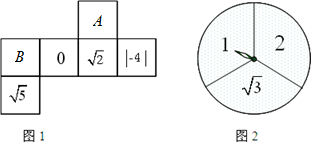
分析：（1）根据题意采用列表法，即可表示出两次自由转动转盘所有可能出现的结果；
（2）依据表格分析所有等可能的出现结果，然后根据概率公式求出该事件的概率．
（2）依据表格分析所有等可能的出现结果，然后根据概率公式求出该事件的概率．
解答：解：（1）所有可能出现的结果如下：
（2）∴总共有9种结果，每种结果出现的可能性都相同，
其中A、B两面上数的乘积大于A对面上的数的结果共有4种：分别是（2，2）、（2，
）、（
，2）、（
，
），
∴A、B两面上数的乘积大于A对面上的数的概率是
．
| B面\A面 | 1 | 2 | y |
| 1 | （1，1） | （1，2） | （1，x） |
| 2 | （2，1） | （2，2） | （2，y） |
| x | （y，1） | （x，2） | （y，x） |
其中A、B两面上数的乘积大于A对面上的数的结果共有4种：分别是（2，2）、（2，
| 3 |
| 3 |
| 3 |
| 3 |
∴A、B两面上数的乘积大于A对面上的数的概率是
| 4 |
| 9 |
点评：本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
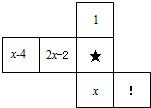8、如图是一个立方体的表面展开图，已知立方体相对两个面上的数值相同，则“★”、“！”面上的数分别为（ ）
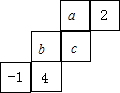如图是一个立方体的表面展开图，已知立方体的每一个面上都有一个实数，且相对面上的两数互为倒数，那么代数式
、|-4|、
；图2是一个可以自由转动的转盘（转盘被分成面积相等的三个扇形），转盘面上分别标有1、2、
．自由转动转盘两次，将第一次转出的数填入图1中的A方格内，将第二次转出的数填入图1中的B方格内．
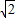、|-4|、
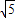；图2是一个可以自由转动的转盘（转盘被分成面积相等的三个扇形），转盘面上分别标有1、2、
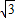．自由转动转盘两次，将第一次转出的数填入图1中的A方格内，将第二次转出的数填入图1中的B方格内．