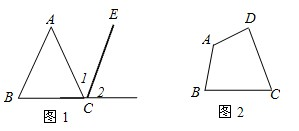题目内容
阅读:如图(1),在△ABC和△DEF中,∠ABC=∠DEF=90°,AB=DE=a,BC=EF=b(a<6),B、C、D、E四点都在直线m上,点B与点D重合,连接AE、FC,我们可以借助于S△ACE和S△FCE的大小关系证明不等式:a2+b2> 2ab(b>a>0)
证明过程如下:
∵BC=b,BE=a,EC=b-a,
∴S△ACE= EC·AB=
EC·AB= (b-a)a,
(b-a)a,
∴S△FCE= EC·FE=
EC·FE= (b-a)b,
(b-a)b,
∵b>a>0,
∴S△FCE >S△ACE,
即 (b-a)b>
(b-a)b> (b-a)a,
(b-a)a,
∴b2-ab>ab-a2
∴a2+b2>2ab。
解决下列问题:
(1)现将△DEF沿直线m向右平移,设BD=k(b-a),且0≤k≤1,如图(2),当BD=EC时,k=____,利用此图,仿照上述方法,证明不等式:a2+b2>2ab(b >a>0);
(2)用四个与△ABC全等的直角三角形纸板进行拼接,也能够借助图形证明上述不等式请你画出一个示意图,并简要说明理由。
证明过程如下:
∵BC=b,BE=a,EC=b-a,
∴S△ACE=
 EC·AB=
EC·AB= (b-a)a,
(b-a)a, ∴S△FCE=
 EC·FE=
EC·FE= (b-a)b,
(b-a)b,∵b>a>0,
∴S△FCE >S△ACE,
即
 (b-a)b>
(b-a)b> (b-a)a,
(b-a)a, ∴b2-ab>ab-a2
∴a2+b2>2ab。
解决下列问题:
(1)现将△DEF沿直线m向右平移,设BD=k(b-a),且0≤k≤1,如图(2),当BD=EC时,k=____,利用此图,仿照上述方法,证明不等式:a2+b2>2ab(b >a>0);
(2)用四个与△ABC全等的直角三角形纸板进行拼接,也能够借助图形证明上述不等式请你画出一个示意图,并简要说明理由。

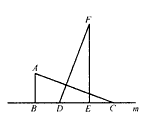
(1) (2)
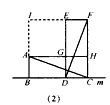
解:(1)k=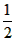 , ,证明:如图(1),连接AD、BF, 可得BD= 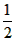 (b-a), (b-a), ∴S△ABD= 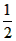 BD·AB= BD·AB=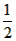 × ×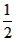 ×(b-a)·a= ×(b-a)·a=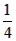 a(b-a), a(b-a),S△FBD= 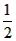 BD·FE= BD·FE=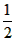 × ×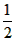 ×(b-a)·b= ×(b-a)·b=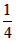 b(b-a), b(b-a),∵b>a>0, ∴S△ABD<S△FBD 即 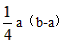 < <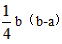 ∴ab-a2<b2-ab ∴a2+b2>2ab, |
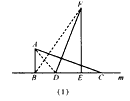 |
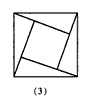
| (2)答案不唯一, 举例:如图(2),理由: 延长BA、FE交于点I, ∵b>a >0, ∴S矩形IBDE> S矩形ABDG, 即b(b-a)>a(b-a), ∴b2-ab> ab-a2 ∴a2+b2 >2ab, 举例:如图(3),理由: 四个直角三角形的面积和S1=4× 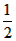 ab=2ab, ab=2ab,大正方形的面积S2=a2+b2 ∵b>a>0, ∴S2>S1 ∴a2+b2>2ab。 |
  |

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目