题目内容
【题目】如图，已知直线y＝x+5与x轴交于点A，直线y＝kx+b与x轴交于点B（1，0），且与直线y＝x+5交于第二象限点C（m，n）．
（1）若△ABC的面积为12，求点C的坐标及关于x的不等式的x+5＞kx+b解集；
（2）求k的取值范围．
【答案】（1）x＞﹣1；（2）﹣5＜k＜0.
【解析】
1）由题意可求点A坐标，由三角形面积关系可求点C坐标，由一次函数性质可求不等式解集；
（2）列出方程组，用参数k表示点C坐标，由点C坐标在第二象限列出不等式组可求k的取值范围．
解：（1）∵直线y＝x+5与x轴交于点A
∴x+5＝0 解得：x＝﹣5
∴A（﹣5，0）
∵B（1，0）
∴AB＝1﹣（﹣5）＝6
∵C（m，n）
∵S△ABC＝
AByC＝×6n＝3n＝12
∴n＝4
∵点C（m，n）在直线AB上
∴m+5＝n＝4
∴m＝﹣1
∴点C坐标为（﹣1，4）
由图象可知，不等式x+5＞kx+b的解集为x＞﹣1．
（2）∵直线y＝kx+b与x轴交于点B（1，0），
∴0＝k+b
∴b＝﹣k
∴y＝kx﹣k
∵直线y＝kx+b与x轴交于点B（1，0），且与直线y＝x+5交于第二象限点C（m，n）．
∴
∴
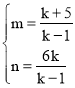
∵m＜0，n＞0
∴﹣5＜k＜0
金状元绩优好卷系列答案
【题目】为积极响应“弘扬传统文化”的号召，万州区某中学举行了一次中学生诗词大赛活动.小何同学对他所在八年级一班参加诗词大赛活动同学的成绩进行了整理，成绩分别100分、90分、80分、70分，并绘制出如下的统计图.
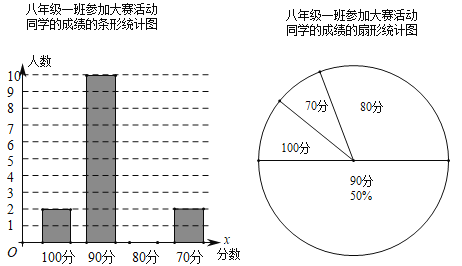
请根据以上提供的信息，解答下列问题：
（1）该校八年级（1）班参加诗词大赛成绩的众数为______分；并补全条形统计图.
（2）求该校八年级（1）班参加诗词大赛同学成绩的平均数；
（3）结合平时成绩、期中成绩和班级预选成绩（如下表），年级拟从该班小何和小王的两位同学中选一名学生参加区级决赛，按
的比例计算两位同学的最终得分，请你根据计算结果确定选谁参加区级决赛.
学生姓名 | 平时成绩 | 期中成绩 | 预选成绩 |
小何 | 80 | 90 | 100 |
小王 | 90 | 100 | 90 |
