题目内容
四边形ABCD中,点E在边CD上,连接AE、BE.设∠EAD=∠1,∠EAB=∠2,∠ABE=∠3,∠CBE=∠4,给出下列五个关系式,①AD∥BC;②DE=CE;③∠1=∠2 ④∠3=∠4;⑤AD+BC=AB;将其中的三个关系作为题设,另外两个作为结论,构成一个命题.
(1)用序号写出一个真命题(书写形式如:如果xxx,那么xxx),并给出证明;
(2)用序号写出三个真命题(不需要证明)
(3)在本题可以书写的命题中,只有一个是假命题,是哪一个?说明理由.
 解:(1)如果①②③,那么④⑤.
解:(1)如果①②③,那么④⑤.证明:延长AE交BC的延长线于点F(如图)
∵AD∥BC,
∴∠1=∠F,∠ADE=∠FCE,
又CE=DE,
∴△ADE≌△FCE,
AE=FE,AD=CF,
∠1=∠2=∠F,
BA=BF,
BA=BC+CF=BC+AD,
AE=EF,
∴∠3=∠4(5分).
(2)如果①②④,那么③⑤;如果①②⑤,那么③④;如果①③④,那么②⑤(9分).

(3)如果②③④,那么①⑤.
如图,ABE和BCE和AED是全等的等边三角形,此时C、D、E在同一直线上,
CE=DE,∠DAE=∠BAE=∠CBE=∠ABE=60°,
但AD与BC不平行(12分).
分析:(1)解答此题的关键是利用已知条件先求证△ADE≌△FCE,然后即可得出结论.
(2)从三角形全等方面分析①②③④⑤中,哪些作为已知条件,哪些作为命题.
(3)假设命题成立,用事实证明去推翻,详细证明(见解答部分)
点评:此题考查学生对全等三角形的判定与性质和等边三角形的判定与性质的理解和掌握,此题如果单纯是证明这些命题成立或不成立,就容易的多,但是让学生自己写命题,就有一定的难度,所以这是一道难题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 15、如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好落在CD上的点F,若△FDE的周长为8,△FCB的周长为14,则FC的长为
15、如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好落在CD上的点F,若△FDE的周长为8,△FCB的周长为14,则FC的长为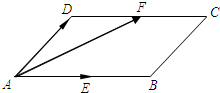 如图,在平行四边形ABCD中,点E、F分别是AB、CD上的中点,记
如图,在平行四边形ABCD中,点E、F分别是AB、CD上的中点,记 (1)如图1,已知平行四边形ABCD中,点E为BC边的中点,延长DE,AB相交于点F.求证:CD=BF.
(1)如图1,已知平行四边形ABCD中,点E为BC边的中点,延长DE,AB相交于点F.求证:CD=BF.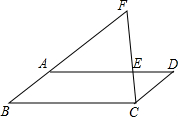 (2013•重庆)如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,CD=3cm,则AF的长为( )
(2013•重庆)如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,CD=3cm,则AF的长为( )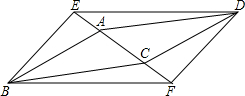 如图,在平行四边形ABCD中,点E、F分别位于对角线CA的延长线与反向延长线上,且AE=CF.
如图,在平行四边形ABCD中,点E、F分别位于对角线CA的延长线与反向延长线上,且AE=CF.