题目内容
如图,已知直线lAC:y=﹣ 交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.
交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.
(1)求点B的坐标及直线BC的解析式;
(2)将△OBC关于BC边翻折,得到△O′BC,过点O′作直线O′E垂直x轴于点E,F是y轴上一点,P是直线O′E上任意一点,P、Q两点关于x轴对称,当|PA﹣PC|最大时,请求出QF+ FC的最小值;
FC的最小值;
(3)若M是直线O′E上一点,且QM=3 ,在(2)的条件下,在平面直角坐标系中,是否存在点N,使得以Q、F、M、N四点为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
,在(2)的条件下,在平面直角坐标系中,是否存在点N,使得以Q、F、M、N四点为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
在一次数学测试中,某小组五名同学的成绩(单位:分)如下表(有两个数据被遮盖).
组员 | 甲 | 乙 | 丙 | 丁 | 戊 | 方差 | 平均成绩 |
得分 | 81 | 79 | ■ | 80 | 82 | ■ | 80 |
那么被遮盖的两个数据依次是( )
A. 80,2 B. 80,10 C. 78,2 D. 78,10


 (2)
(2)
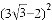 (4)
(4)

 +
+ +
+ ,则
,则 的值为_____.
的值为_____.

 x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点An的坐标为__.
x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点An的坐标为__.