题目内容
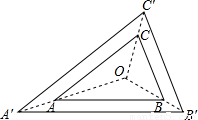
 如图,Rt△ABC与Rt△A′B′C′是位似图形,点O是位似中心,若OA=
如图,Rt△ABC与Rt△A′B′C′是位似图形,点O是位似中心,若OA= OA′,S△ABC=8,则S△A′B′C′等于
OA′,S△ABC=8,则S△A′B′C′等于
- A.4
- B.12
- C.18
- D.24
C
分析:根据位似图形的定义与性质由Rt△ABC与Rt△A′B′C′是位似图形,得到Rt△ABC∽Rt△A′B′C′,利用相似三角形的性质得到S△ABC:S△A′B′C′=OA2:OA′2,然后把OA= OA′,S△ABC=8代入进行计算即可得到∴S△A′B′C′的值.
OA′,S△ABC=8代入进行计算即可得到∴S△A′B′C′的值.
解答:∵Rt△ABC与Rt△A′B′C′是位似图形,
∴Rt△ABC∽Rt△A′B′C′,
∴S△ABC:S△A′B′C′=OA2:OA′2,
而OA= OA′,S△ABC=8,
OA′,S△ABC=8,
∴8:S△A′B′C′=4:9,
∴S△A′B′C′=18.
故选C.
点评:本题考查了位似图形的定义与性质:如果两个图形不仅是相似图形,而且每组对应点的连线交于一点,对应边互相平行或在一条直线上,那么这两个图形叫位似图形,这个点叫做位似中心,这时的相似比又称为位似比. 位似图形的对应点和位似中心在同一直线上,它们到位似中心的距离之比等于相似比.
分析:根据位似图形的定义与性质由Rt△ABC与Rt△A′B′C′是位似图形,得到Rt△ABC∽Rt△A′B′C′,利用相似三角形的性质得到S△ABC:S△A′B′C′=OA2:OA′2,然后把OA=
 OA′,S△ABC=8代入进行计算即可得到∴S△A′B′C′的值.
OA′,S△ABC=8代入进行计算即可得到∴S△A′B′C′的值.解答:∵Rt△ABC与Rt△A′B′C′是位似图形,
∴Rt△ABC∽Rt△A′B′C′,
∴S△ABC:S△A′B′C′=OA2:OA′2,
而OA=
 OA′,S△ABC=8,
OA′,S△ABC=8,∴8:S△A′B′C′=4:9,
∴S△A′B′C′=18.
故选C.
点评:本题考查了位似图形的定义与性质:如果两个图形不仅是相似图形,而且每组对应点的连线交于一点,对应边互相平行或在一条直线上,那么这两个图形叫位似图形,这个点叫做位似中心,这时的相似比又称为位似比. 位似图形的对应点和位似中心在同一直线上,它们到位似中心的距离之比等于相似比.

练习册系列答案
相关题目

 如图,Rt△ABC与Rt△A′B′C′是位似图形,点O是位似中心,若OA=
如图,Rt△ABC与Rt△A′B′C′是位似图形,点O是位似中心,若OA= 如图,Rt△ABC与Rt△A′B′C′关于直线l对称,则线段AC的长为( )
如图,Rt△ABC与Rt△A′B′C′关于直线l对称,则线段AC的长为( )
 OA′,S△ABC=8,则S△A′B′C′等于( )
OA′,S△ABC=8,则S△A′B′C′等于( )