题目内容
已知矩形A的边长分别为a和b，如果总有另一矩形B，使得矩形B与矩形A的周长之比与面积之比都等于k，则k的最小值为 ．
【答案】分析：先根据矩形的性质，列出一元二次方程，再利用根的判别式求根即可．
解答：解：设矩形B的边长分别为x和y
根据题意：
xy=kab，
x+y=k（a+b），
将y=k（a+b）-x代入xy=kab中，
x2-k（a+b）x+kab=0，
利用一元二次方程求根公式：
x=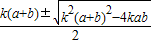
，
△=k2（a+b）2-4kab≥0条件下，x才有解，
由上面这个不等式推出：
k≥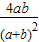
，
∴k的最小值为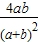
．
点评：本题的关键是利用面积周长比列出方程组成一个一元二次方程，用根的判别式求根的情况．
解答：解：设矩形B的边长分别为x和y
根据题意：
xy=kab，
x+y=k（a+b），
将y=k（a+b）-x代入xy=kab中，
x2-k（a+b）x+kab=0，
利用一元二次方程求根公式：
x=
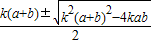，△=k2（a+b）2-4kab≥0条件下，x才有解，
由上面这个不等式推出：
k≥
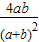，∴k的最小值为
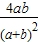．点评：本题的关键是利用面积周长比列出方程组成一个一元二次方程，用根的判别式求根的情况．
练习册系列答案
名校课堂系列答案
相关题目
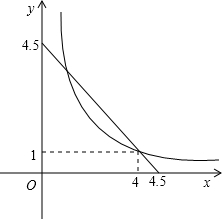由题意得方程组：
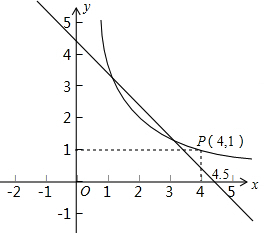（2012•西城区模拟）探索一个问题：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”