题目内容
【题目】已知线段AB=12,CD=6,线段CD在直线AB上运动(A在B的左侧,C在D的左侧).
(1)当D点与B点重合时,AC=_________;
(2)点P是线段AB延长线上任意一点,在(1)的条件下,求PA+PB–2PC的值;
(3)M、N分别是AC、BD的中点,当BC=4时,求MN的长.
![]()
【答案】(1)6;(2)PA+PB–2PC=0;(3)MN=9.
【解析】分析:(1)根据题意即可得到结论;(2)由(1)得AC=![]() AB,CD=
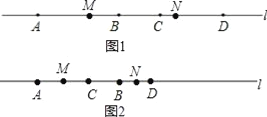
AB,CD=![]() AB,根据线段的和差即可得到结论;(3)需要分类讨论:①如图1,当点C在点B的右侧时,根据“M、N分别为线段AC、BD的中点”,先计算出AM、DN的长度,然后计算MN=AD-AM-DN;②如图2,当点C位于点B的左侧时,利用线段间的和差关系求得MN的长度.
AB,根据线段的和差即可得到结论;(3)需要分类讨论:①如图1,当点C在点B的右侧时,根据“M、N分别为线段AC、BD的中点”,先计算出AM、DN的长度,然后计算MN=AD-AM-DN;②如图2,当点C位于点B的左侧时,利用线段间的和差关系求得MN的长度.
本题解析:
(1)当D点与B点重合时,AC=AB﹣CD=6;
故答案为:6;
(2)由(1)得AC=![]() AB,
AB,
∴CD=![]() AB,
AB,
∵点P是线段AB延长线上任意一点,
∴PA+PB=AB+PB+PB,PC=CD+PB=![]() AB+PB,
AB+PB,
∴PA+PB﹣2PC=AB+PB+PB﹣2(![]() AB+PB)=0;
AB+PB)=0;
(3)如图1,∵M、N分别为线段AC、BD的中点,
∴AM=![]() AC=
AC=![]() (AB+BC)=8,
(AB+BC)=8,
DN=![]() BD=
BD=![]() (CD+BC)=5,
(CD+BC)=5,
∴MN=AD﹣AM﹣DN=9;
如图2,∵M、N分别为线段AC、BD的中点,
∴AM=![]() AC=
AC=![]() (AB﹣BC)=4,
(AB﹣BC)=4,
DN=![]() BD=
BD=![]() (CD﹣BC)=1,
(CD﹣BC)=1,
∴MN=AD﹣AM﹣DN=12+6﹣4﹣4﹣1=9.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目