��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�������![]() ��x�ύ�ڵ�A(-4,0)��B(6,0�����㣬��y�ύ�ڵ�C��
��x�ύ�ڵ�A(-4,0)��B(6,0�����㣬��y�ύ�ڵ�C��
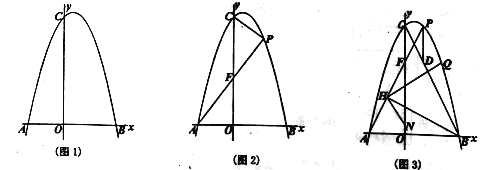
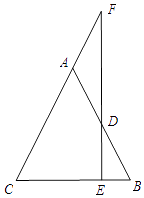
(1)��ͼl���������ߵĽ���ʽ��
(2)��ͼ2����PΪ��һ������������һ�㣬����PC��PA��PA��y���ڵ�F�����P�ĺ�����Ϊt����CPF�����ΪS����S��t�ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
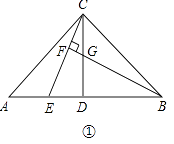
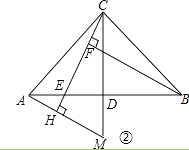
(3)��ͼ3����(2)�������£�����BC������P��PD//y���BC�ڵ�D����HΪAF�е㣬�ҵ�N(0��1)������NH��BH������NHB�Ƶ�H��ʱ����ת��ʹ�ǵ�һ����H��������HF��,��һ����HN���������ڵ�Q����BH=BDʱ�����Q���꣮
���𰸡���1�������ߵĽ���ʽΪ![]() ��
��
��2��S��t�ĺ�����ϵʽΪ![]() ��
��
��3����Q������4��8��.
�������������������1��ֱ���ô��뷨�����Ľ���ʽ����2������P��PR��y�ᣬ��y���ڵ�R������P��PL��AB�ڵ�L�����P(t, ![]() )����Rt��PAL�У���ΪPL=
)����Rt��PAL�У���ΪPL=![]() AL=
AL= ![]() ������tan��PAL=
������tan��PAL=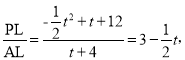 ��Rt��FAO������tan��FAO=
��Rt��FAO������tan��FAO= ![]() , ����OF=12-2t������CF=CO- OF=12-��12-2t��=2t������
, ����OF=12-2t������CF=CO- OF=12-��12-2t��=2t������![]() ����3���ӳ�PD��x���ڵ�L��ȡOA���е�K������HK,����H��HG��y���ڵ�G��OF��12-2t��HΪAF���е� HK ��OA ������HK=
����3���ӳ�PD��x���ڵ�L��ȡOA���е�K������HK,����H��HG��y���ڵ�G��OF��12-2t��HΪAF���е� HK ��OA ������HK=![]() 6-t=BL����ΪHK=BL BH=BD �����ԡ�BHK�ա�DBL ������BK=DL=8��ֱ��BC�Ľ���ʽΪ
6-t=BL����ΪHK=BL BH=BD �����ԡ�BHK�ա�DBL ������BK=DL=8��ֱ��BC�Ľ���ʽΪ![]() ���D
���D![]() ��DL=12-2t =8 t=2 �����Ե�P��2��12�������H��-2��4����tan��AHK=tan��HBK=
��DL=12-2t =8 t=2 �����Ե�P��2��12�������H��-2��4����tan��AHK=tan��HBK=![]() �����ԡ�AHK=��HBK �����AHB=90��������Ϊ��NHB=��PHQ �����ԡ�NHQ=90��������Q��QM��HG�ڵ�M�����ԡ�HNG=��QHM ������Ϊ��N��0��1����HG=2������GN=3��tan��HNG=tan��QHM =
�����ԡ�AHK=��HBK �����AHB=90��������Ϊ��NHB=��PHQ �����ԡ�NHQ=90��������Q��QM��HG�ڵ�M�����ԡ�HNG=��QHM ������Ϊ��N��0��1����HG=2������GN=3��tan��HNG=tan��QHM =![]() ��
�� ![]() �����Q(
�����Q(![]() ,
,![]() ) ����QM=
) ����QM=![]() -4=
-4=![]() ������HM=
������HM= ![]() +2 ������
+2 ������  ����ã�
����ã� ![]() ������ ���Q��4��8����
������ ���Q��4��8����
���������
��1�����������![]() ����A��-4��0����B��6��0��
����A��-4��0����B��6��0��
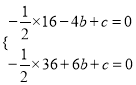 ���
���![]()
�������߽���ʽΪ![]()
��2������P��PR��y�ᣬ��y���ڵ�R������P��PL��AB�ڵ�L����ͼ��ʾ��
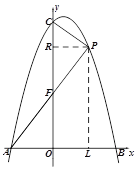
���P(t, ![]() )����Rt��PAL��
)����Rt��PAL��
��PL=![]() AL=
AL= ![]()
��tan��PAL= 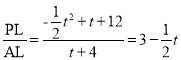
��Rt��FAO��
��tan��FAO= ![]() ,
,
��OF=12-2t
��CF=CO- OF=12-��12-2t��=2t
��![]()
��3���ӳ�PD��x���ڵ�L��ȡOA���е�K������HK,����H��HG��y���ڵ�G����ͼ��ʾ��
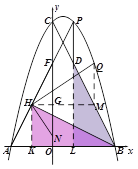
OF��12-2t��HΪAF���е� HK ��OA
��HK=![]() 6-t=BL
6-t=BL
��HK=BL BH=BD
���BHK�ա�DBL
��BK=DL=8
ֱ��BC�Ľ���ʽΪ![]() ����
����
���D![]()
DL=12-2t =8 t=2
���P��2��12��
���H��-2��4��
tan��AHK=tan��HBK=
���AHK=��HBK
���AHB=90��
�ߡ�NHB=��PHQ
���NHQ=90����
����Q��QM��HG�ڵ�M��
���HNG=��QHM
�ߵ�N��0��1����HG=2��
��GN=3��tan��HNG=tan��QHM =![]() ��
�� ![]()
���Q(![]() ,
,![]() )
)
QM=![]() -4=
-4=![]()
HM= ![]() +2
+2
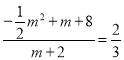 ��
��
![]()
���Q��4��8��

 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�