题目内容
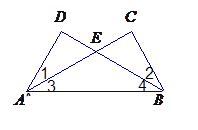
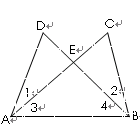
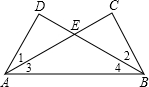 如图,给出下列论断:①DE=CE,②∠1=∠2,③∠3=∠4.请你将其中的两个作为条件,另一个作为结论,构成一个真命题,并加以证明.
如图,给出下列论断:①DE=CE,②∠1=∠2,③∠3=∠4.请你将其中的两个作为条件,另一个作为结论,构成一个真命题,并加以证明.
分析:可以有三个真命题:
(1)②③?①,可由ASA证得△ADE≌△BCE,所以DE=EC;
(2)①③?②,可由SAS证得△ADE≌△BCE,所以∠1=∠2;
(3)①②?⑧,可由ASA证得△ADE≌△BCE,所以AE=BF,∠3=∠4.
(1)②③?①,可由ASA证得△ADE≌△BCE,所以DE=EC;
(2)①③?②,可由SAS证得△ADE≌△BCE,所以∠1=∠2;
(3)①②?⑧,可由ASA证得△ADE≌△BCE,所以AE=BF,∠3=∠4.
解答:解:②③?①
证明如下:
∵∠3=∠4,
∴EA=EB.
在△ADE和△BCE中,
∴△ADE≌△BCE.
∴DE=EC.
①③?②
证明如下:
∵∠3=∠4,
∴EA=EB,
在△ADE和△BCE中,
,
∴△ADE≌△BCE,
∴∠1=∠2.
①②?⑧
证明如下:
在△ADE和△BCE中,
∴△ADE≌△BCE.
∴AE=BE,∠3=∠4.
证明如下:
∵∠3=∠4,
∴EA=EB.
在△ADE和△BCE中,
|
∴△ADE≌△BCE.
∴DE=EC.
①③?②
证明如下:
∵∠3=∠4,
∴EA=EB,
在△ADE和△BCE中,
|
∴△ADE≌△BCE,
∴∠1=∠2.
①②?⑧
证明如下:
在△ADE和△BCE中,
|
∴△ADE≌△BCE.
∴AE=BE,∠3=∠4.
点评:本题考查了全等三角形的判定和性质;题目是一道开放型的问题,选择有多种,可以采用多次尝试法,证明时要选择较为简单的进行证明.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
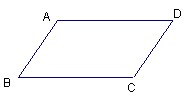 21、如图,给出下列论断:(1)AB∥DC;(2)AD∥BC;(3)∠A+∠B=180°;(4)∠B+∠C=180度.以其中一个作题设,一个作结论,写出一个真命题:
21、如图,给出下列论断:(1)AB∥DC;(2)AD∥BC;(3)∠A+∠B=180°;(4)∠B+∠C=180度.以其中一个作题设,一个作结论,写出一个真命题: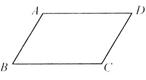
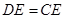 ,②
,②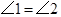 ,③
,③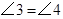 .请你将其中的两个作为条件,另一个作为结论,使结论成立,并说明理由.
.请你将其中的两个作为条件,另一个作为结论,使结论成立,并说明理由.