题目内容
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E是AD边上的动点,将矩形ABCD沿BE折叠,点A落在点A′处,连接A′C、BD.
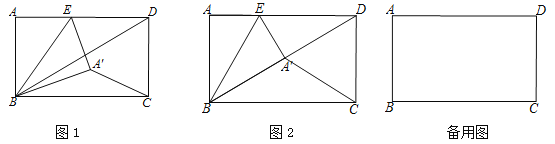
(1)如图1,若点A′恰好落在BD上,求tan∠ABE的值;
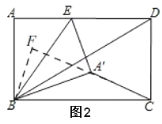
(2)如图2,已知AE=2,求△A′CB的面积;
(3)点E在AD边上运动的过程中,∠A′CB的度数是否存在最大值,若存在,求出此时线段AE的长;若不存在,请说明理由.
【答案】(1)![]() ;(2)19.2;(3)
;(2)19.2;(3)![]() .
.
【解析】
(1)先根据勾股定理得,BD=10,最后用勾股定理建立方程求解即可得出结论;
(2)过点A’作FH⊥AD,A’G⊥AB,设A’F=x,证明△FEA’∽GBA’,列出比例式求出x的值,然后求出A’H,代入三角形面积公式进行计算;
(3)先判断出∠A'CB最大时,点A'在CE上,进而利用三角形的面积求出CE,进而用勾股定理求出DE,即可得出结论.
解:(1)∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=8,
在Rt△ABD中,根据勾股定理得,BD=10,
设AE=x,
∴DE=ADAE=8x,
由折叠知,A'E=AE=x,A'B=AB=6,∠BA'E=∠A=90°,
∴A'D=BDA'B=4,
∴∠DA'E=90°,
在Rt△DA'E中,根据勾股定理得,DE2A'E2=A'D2=16,
∴(8x)2x2=16,
∴x=3,
∴AE=3,
在Rt△ABE中,tan∠ABE=![]() ;
;
(2)在四边形ABA’E中,∠ABA’=180°-∠AEA’,而∠DEA’=180°-∠AEA’,
∴∠ABA’=∠DEA’,
如图1,过点A’作FH⊥AD,A’G⊥AB,设A’F=x,则EF=![]() ,
,
则FH⊥BC,△FEA’∽GBA’,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴A’H=![]() ,
,
∴S△A′CB=![]()
(3)∠A′CB的度数存在最大值,
理由:如图2,过点B作BF⊥CA'交CA'的延长线于F,
在Rt△BFC中,sin∠A'CB=![]() ,
,
∴BF越大时,sin∠A'CB越大,即∠A'CB越大,
当点E在边AD上运动时,点A'与F重合时,BF最大=A'B=AB=6,
∴A'B⊥A'C,
∴∠BA'C=90°,
由折叠知,∠BA'E=∠A=∠D=90°,
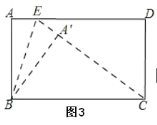
∴点A'在CE上,如图3,
∵四边形ABCD是矩形,
∴∠D=∠A=90°,CD=AB=6,
根据三角形面积得,Sspan>△BCE=![]() BCAB=
BCAB=![]() CEA'B,
CEA'B,
∵A'B=AB,
∴CE=BC=8,
在Rt△CDE中,根据勾股定理DE=![]() ,
,
∴AE=ADDE=8![]() .
.


 阅读快车系列答案
阅读快车系列答案【题目】为了传承中华优秀传统文化,某校学生会组织了一次全校1200名学生参加的“汉字听写”大赛,并设成绩优胜奖.
赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中100名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.10 |
60≤x<70 | 25 | 0.25 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.20 |
90≤x≤100 | 15 | 0.15 |
成绩在70≤x<80这一组的是:
70 70 71 71 71 72 72 73 73 73 73 75 75 75 75 76 76 76 76 76 76 76 76 77 77 78 78 78 79 79
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数是 ;
(4)若这次比赛成绩在78分以上(含78分)的学生获得优胜奖,则该校参加这次比赛的1200名学生中获优胜奖的约有多少人?