题目内容
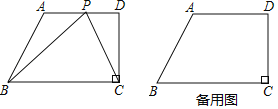
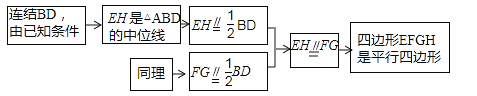
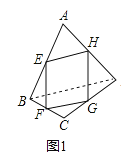
【题目】如图①,已知点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,求证四边形FFG是平行四边形.根据以下思路可以证明四边形EFGH是平行四边形:
(1)根据上述思路,请你写出完整的证明过程;
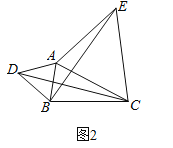
(2)如图,已知![]() ,分别以AB、AC为边,在BC同侧作等边三角形ABD和等边三角形ACE,连接CD,BF.可通过证明△________≌△________,得到
,分别以AB、AC为边,在BC同侧作等边三角形ABD和等边三角形ACE,连接CD,BF.可通过证明△________≌△________,得到![]() ;
;
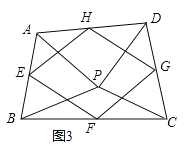
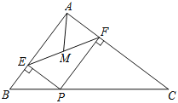
(3)如图③,点P是四边形ABCD内一点,且满足![]() ,
,![]() ,
,![]() ,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想四边形EFGH的形状,并证明.
,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想四边形EFGH的形状,并证明.
【答案】(1)见解析;(2)ADC,ABE;(3)四边形EFGH为菱形,理由见解析
【解析】
(1)连接BD,根据三角形的中位线的性质得到![]() ∥
∥![]() ,
,![]() ,由平行四边形的判定定理即可得到结论;
,由平行四边形的判定定理即可得到结论;
(2)先利用等边三角形的性质得AD=AB,AC=AE,∠BAD=∠CAE=60°,则∠DAC=∠BAE,于是根据![]() 证得
证得![]() ,从而得到结论;
,从而得到结论;
(3)连接AC、BD,如图3,先证明△PBD≌△APC得到BD=AC,再利用三角形中位线性质得到HG=HE,接着根据(1)中结论和菱形的判定方法可判断四边形EFGH为菱形.
(1)∵点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,
∴EH是![]() 的中位线,FG是
的中位线,FG是![]() 的中位线,
的中位线,
∴![]() ∥
∥![]() ,
,![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,
∴![]() ∥
∥![]() ,
,![]() ,
,
∴四边形EFGH是平行四边形;
(2)ADC,ABE;
理由是:
∵![]() 和
和![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中,
∴![]() ,
,
∴![]() .
.
(3)四边形EFGH为菱形
如图,连接AC、BD,

∵![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∵由(1)中的结论可知,四边形EFGH为平行四边形,
∴四边形EFCH为菱形.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目