题目内容
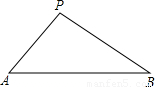
如图，在凯里市某广场上空飘着一只汽球P，A、B是地面上相距90米的两点，它们分别在汽球的正西和正东，测得仰角∠PAB=45°，仰角∠PBA=30°，求汽球P的高度．（精确到0.1米，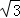
=1.732）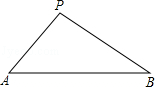
见解析解析:
作PC⊥AB于C点，设PC=x米．
在Rt△PAC中，tan∠PAB=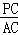
，
∴AC=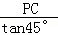
=PC=x．
在Rt△PBC中，tan∠PBA=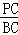
，
∴BC=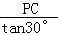
=
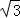x．
又∵AB=90，
∴AB=AC+BC=x+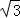x=90，
∴
，
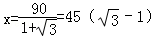∴PC=45（1.732﹣1）=32.9．
答：汽球P的高度为32.9米．
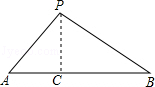
作PC⊥AB于C点，设PC=x米．
在Rt△PAC中，tan∠PAB=
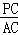，∴AC=
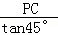=PC=x．在Rt△PBC中，tan∠PBA=
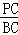，∴BC=
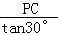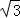=x．又∵AB=90，
∴AB=AC+BC=x+
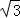x=90，∴
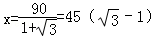，∴PC=45（1.732﹣1）=32.9．
答：汽球P的高度为32.9米．
练习册系列答案
相关题目
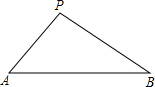如图，在凯里市某广场上空飘着一只气球P，A、B是地面上相距90米的两点，它们分别在汽球的正西和正东，测得仰角∠PAB=45°，仰角∠PBA=30°，求汽球P的高度．（精确到0.1米，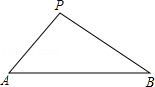
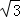=1.732）
=1.732）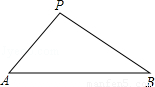
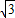=1.732）