Question

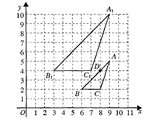
如图，已知图中每个小正方形的边长为1，则点C到AB所在直线的距离等于

2

．

Answer 1

分析：首先根据勾股定理可求得三角形各边的长，利用勾股定理逆定理得到该三角形是直角三角形，再根据三角形的面积公式即可算出点C到AB所在直线的距离．

解答：解：根据勾股定理求得：AC=

42+22

=2

5

，BC=

22+12

=

5

，AB=

32+42

=5，
∵（2

5

）²+（

5

）²=5²，
∴AC²+CB²=AB²，
∴∠ACB=90°，
∴△ACB的面积为：

1

2

AC×CB=

1

2

×2

5

×

5

=5，
设点C到AB所在直线的距离为h，
∴

1

2

×AB×h=5，

1

2

×5×h=5，
h=2．
故答案为：2．

点评：此题主要考查了勾股定理，勾股定理逆定理，以及三角形的面积公式，解决问题的关键是证明△ACB是直角三角形，再根据三角形的面积不变进一步求得斜边上的高．