Question

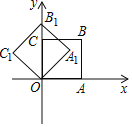
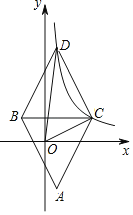
【题目】如图，在平面直角坐标系中，菱形ABDC的顶点D，C在反比例函数y＝上（k＞0，x＞0），横坐标分别为和2，对角线BC∥x轴，菱形ABDC的面积为9．

（1）求k的值及直线CD的解析式；

（2）连接OD，OC，求△OCD的面积．

Answer 1

【答案】（1）k=2，y＝﹣2x+5；（2）．

【解析】

（1）连接AD，与BC交于点M，由点D，C横坐标分别为和2，得到CM＝，根据菱形的面积得到DM＝3，设C（2，m），则D（，m+3），列方程得到k＝2，求得D（，4），设直线CD的解析式为：y＝kx+b，解方程即可得到结论；

（2）设AD与x轴交于N，过C作CH⊥x轴于H，根据S△COD＝S四边形DNHC于是得到结论．

解：（1）连接AD，与BC交于点M，

∵菱形对角线BC∥x轴，

∴AD⊥BC，

∵点D，C横坐标分别为和2，

∴CM＝，

∵菱形ABCD的面积为9，

∴2DMCM＝9，

∴DM＝3，

设C（2，m），则D（，m+3），

∵D，C在反比例函数y＝的图象上，

∴2m＝（m+3），

∴m＝1，

∴C（2，1），

∴k＝2，

∴D（，4），

设直线CD的解析式为：y＝kx+b，

∴，

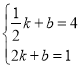解得：，

∴直线CD的解析式为y＝﹣2x+5；

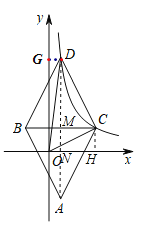
（2）设AD与x轴交于N，过C作CH⊥x轴于H.

∵S△NOD＝S△COH＝×2=1，

∴S△COD＝S四边形DNHC＝（1+4）×＝．