题目内容
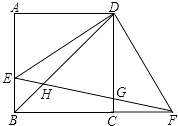
【题目】如图,已知:正方形ABCD中,AB=8,点O为边AB上一动点,以点O为圆心,OB为半径的⊙O交边AD于点E(不与点A、D重合),EF⊥OE交边CD于点F.设BO=x,AE=y.
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)在点O运动的过程中,△EFD的周长是否发生变化?如果发生变化,请用x的代数式表示△EFD的周长;如果不变化,请求出△EFD的周长;
(3)以点A为圆心,OA为半径作圆,在点O运动的过程中,讨论⊙O与⊙A的位置关系,并写出相应的x的取值范围.

【答案】(1)![]()
(2)△EFD的周长不变.理由见解析;
(3)当⊙O与⊙A相交时, ![]() ;当⊙O与⊙A内切时,
;当⊙O与⊙A内切时, ![]() ;当⊙O与⊙A内含时,
;当⊙O与⊙A内含时, ![]()
【解析】试题分析: (1)OB、OE均是 O的半径,得出OB=OE,然后在Rt△AOE中,运用勾股定理可得出y与x的关系式,结合二次根式有意义的条件,可得出x的范围;
(2)先判断△AOE∽△DEF,然后根据相似三角形的周长之比等于相似比,可得出△DEF周长的表达式,进一步化简可得出答案;
(3)设 O的半径R1=x,则 A的半径R2=8-x,圆心距d=OA=8-x,分三种情况讨论,依此解出x的范围即可.
试题解析:(1)∵以点O为圆心,OB为半径的⊙O交边AD于点E,
∴OB=OE,
∵四边形ABCD是正方形,
∴∠A=90°,
∴AO2+AE2=OE2,即(8-x)2+y2=x2,
∵y>0,
∴![]()
(2)△EFD的周长不变.
理由如下:
∵EF⊥OE,
∴∠AEO+∠DEF=90°,
∵∠D=∠A=90°,
∴∠AEO+∠AOE=90°,
∴∠DEF=∠AOE,
∴△AOE∽△DEF,
∴![]() =
=![]()
∴![]() =16
=16
(3)设⊙O的半径R1=x,则⊙A的半径R2=8-x,圆心距d=OA=8-x,
∵4<x<8,
∴R1>R2,
因为点A始终在⊙O内,所以外离和外切都不可能;
当⊙O与⊙A相交时,R1-R2<d<R1+R2,即x-8+x<8-x<x+8-x,
解得: ![]()
故可得此时: ![]()
②当⊙O与⊙A内切时,d=R1-R2,即8-x=x-8+x,
解得:x=![]()
③当⊙O与⊙A内含时,0<d<R1-R2,即0<8-x<x-8+x,
解得: ![]()