Question

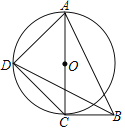
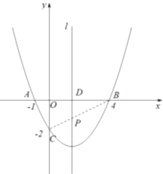
【题目】如图．抛物线经过三点．

（1）求抛物线的函数关系式;

（2）若直线是抛物线的对称轴，设点是直线上的一个动点，当的周长最小时，求点的坐标;

（3）在线段上是否存在点，使得以线段为直径的圆与边交于点(与点不同)，且以点为顶点的三角形是等腰三角形?若存在，求出的值；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）点的坐标为；（3）的值为或．

【解析】

（1）直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可．
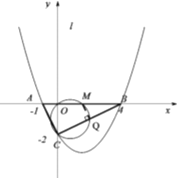
（2）由图知：A、B点关于抛物线的对称轴对称，那么根据抛物线的对称性以及两点之间线段最短可知：若连接BC，那么BC与直线l的交点即为符合条件的P点．
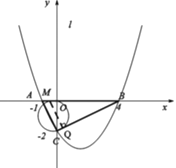
（3）由于△QBO的腰和底没有明确，因此要分三种情况来讨论：①QB=BO、②QB=QO、③QO=BO；可先设出M点的坐标，然后用M点纵坐标表示△QBO的三边长，再按上面的三种情况列式求解即可．

解：经过

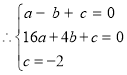
解之得：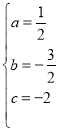

函数解析式为

如图，抛物线的对称轴是直线

当点落在线段上时，

最小，的周长最小．

设抛物线的对称轴与轴的交点为

又，得

由

得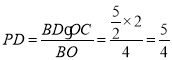

所以点的坐标为

过点作交于点

则根据直径所对圆周角是直角的性质，知点在以为直径的圆上

由

可证是直角三角形

得

由可得

则

由，得

分三种情况：

①当时，

点在垂直平分线上，是的中点，

得．

解得

②当时，

解得：

③当时，

由于，

从而点在的延长线上，

这样点不在线段上

综上所述，的值为或．