题目内容
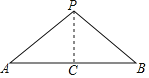
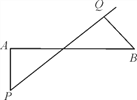
【题目】如图,B地在A地的正东方向,两地相距28![]() km.A,B两地之间有一条东北走向的高速公路,且A,B两地到这条高速公路的距离相等.上午8:00测得一辆在高速公路上行驶的汽车位于A地的正南方向P处,至上午8:20,B地发现该车在它的西北方向Q处,该段高速公路限速为110 km/h.问:该车是否超速行驶?
km.A,B两地之间有一条东北走向的高速公路,且A,B两地到这条高速公路的距离相等.上午8:00测得一辆在高速公路上行驶的汽车位于A地的正南方向P处,至上午8:20,B地发现该车在它的西北方向Q处,该段高速公路限速为110 km/h.问:该车是否超速行驶?
【答案】该车超速行驶了
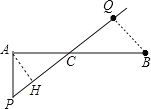
【解析】试题分析:根据题意得到AB=28![]() ,∠P=45°,∠PAC=90°,∠ABQ=45°,则∠ACP=45°,∠BCQ=45°,作AH⊥PQ于H,根据题意有AH=BQ,再证明△ACH≌△BCQ,
,∠P=45°,∠PAC=90°,∠ABQ=45°,则∠ACP=45°,∠BCQ=45°,作AH⊥PQ于H,根据题意有AH=BQ,再证明△ACH≌△BCQ,
得到AC=BC=![]() AB=14
AB=14![]() ,根据等腰直角三角形的性质得PC=
,根据等腰直角三角形的性质得PC=![]() AC=28,CQ=
AC=28,CQ=![]() =14,所以PQ=PC+CQ=42,然后根据速度公式计算出该车的速度=126km/h,再与110km/h比较即可判断该车超速行驶了.
=14,所以PQ=PC+CQ=42,然后根据速度公式计算出该车的速度=126km/h,再与110km/h比较即可判断该车超速行驶了.
试题解析:
根据题意可得,AB=28![]() ,∠P=45°,∠PAC=90°,∠ABQ=45°,
,∠P=45°,∠PAC=90°,∠ABQ=45°,
∴∠ACP=45°,
∴∠BCQ=45°,
作AH⊥PQ于H,则AH=BQ,
在△ACH和△BCQ中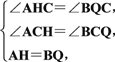
∴△ACH≌△BCQ(AAS),
∴AC=BC=![]() AB=14
AB=14![]() ,
,
∴PC=![]() AC=28,CQ=
AC=28,CQ=![]() =14,
=14,
∴PQ=PC+CQ=42,
∴该车的速度=![]() =126(km/h),
=126(km/h),
∵126 km/h>110 km/h,
∴该车超速行驶了

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
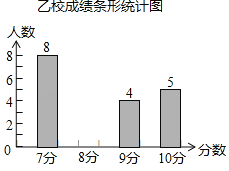
小学生10分钟应用题系列答案【题目】甲、乙两校参加学生英语口语比赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分),乙校平均分是8.3分,乙校的中位数是8分.依据统计数据绘制了如下尚不完整的甲校成绩统计表和乙校成绩统计图;
甲校成绩统计表
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | ■ | 8 |
(1)请你将乙校成绩统计图直接补充完整;
(2)请直接写出甲校的平均分是 ,甲校的中位数是 ,甲校的众数是 ,从平均分和中位数的角度分析 校成绩较好(填“甲”或“乙”).