题目内容
(1999•河北)如图,正方形OABC的顶点O在坐标原点,且OA和AB边所在的直线的解析式分别为:y= x和y=-
x和y=- x+
x+ .D、E分别为边OC和AB的中点,P为OA边上一动点(点P与点O不重合),连接DE和CP,其交点为Q.
.D、E分别为边OC和AB的中点,P为OA边上一动点(点P与点O不重合),连接DE和CP,其交点为Q.(1)求证:点Q为△COP的外心;
(2)求正方形OABC的边长;
(3)当⊙Q与AB相切时,求点P的坐标.

【答案】分析:(1)要证点Q为△COP的外心,需证QC=QP=QO,而△COP中,DQ为中位线,则即可得证;
(2)由OA和AB边的解析式求出A点坐标,由两点之间坐标公式求出OA的长,即正方形边长;
(3)当⊙Q与AB相切时,作出⊙Q,由切线和割线的关系,求出P点坐标.
解答: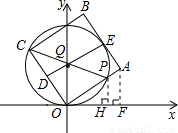 (1)证明:∵D、E分别为正方形OABC中OC、AB的中点,
(1)证明:∵D、E分别为正方形OABC中OC、AB的中点,
∴DE∥OA.
∴Q也是CP的中点.
又∵CP是Rt△COP的斜边,
∴点Q为△COP的外心.
(2)解:由方程组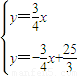
解得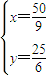 ,
,
∴点A的坐标为(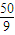 ,
,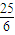 ).
).
过点A作AF⊥Ox轴,垂足为点F.
∴OF=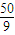 ,AF=
,AF=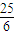 .
.
由勾股定理,得OA=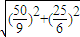 =
=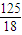 .
.
∴正方形OABC的边长为 .
.
(3)解:如图,当△COP的外接圆⊙Q与AB相切时,
∵圆心Q在直线DE上,DE⊥AB,
∴E为⊙Q与AB相切的切点.
又∵AE和APO分别是⊙Q的切线与割线,
∴AE2=AP•AO.
∵OA=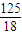 ,AE=
,AE= OA,
OA,
∴AP= OA=
OA=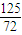 ,
,
∴当⊙Q与AB相切时,OP=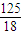 -
-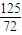 =
=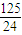 ,
,
作PH⊥Ox轴,垂足为H.
∵PH∥AF,∴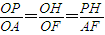
∴OH=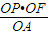 =
=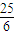 ,
,
PH=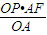 =
=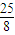
∴点P的坐标为( ,
,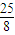 ).
).
点评:本题考查的问题较为复杂,是一次函数和几何知识相结合的问题,同学们要注意几何知识的熟练掌握.
(2)由OA和AB边的解析式求出A点坐标,由两点之间坐标公式求出OA的长,即正方形边长;
(3)当⊙Q与AB相切时,作出⊙Q,由切线和割线的关系,求出P点坐标.
解答:
 (1)证明:∵D、E分别为正方形OABC中OC、AB的中点,
(1)证明:∵D、E分别为正方形OABC中OC、AB的中点,∴DE∥OA.
∴Q也是CP的中点.
又∵CP是Rt△COP的斜边,
∴点Q为△COP的外心.
(2)解:由方程组
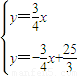
解得
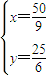 ,
,∴点A的坐标为(
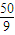 ,
,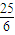 ).
).过点A作AF⊥Ox轴,垂足为点F.
∴OF=
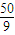 ,AF=
,AF=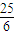 .
.由勾股定理,得OA=
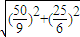 =
=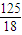 .
.∴正方形OABC的边长为
 .
.(3)解:如图,当△COP的外接圆⊙Q与AB相切时,
∵圆心Q在直线DE上,DE⊥AB,
∴E为⊙Q与AB相切的切点.
又∵AE和APO分别是⊙Q的切线与割线,
∴AE2=AP•AO.
∵OA=
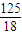 ,AE=
,AE= OA,
OA,∴AP=
 OA=
OA=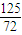 ,
,∴当⊙Q与AB相切时,OP=
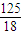 -
-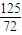 =
=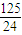 ,
,作PH⊥Ox轴,垂足为H.
∵PH∥AF,∴
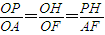
∴OH=
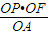 =
=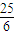 ,
,PH=
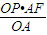 =
=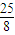
∴点P的坐标为(
 ,
,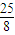 ).
).点评:本题考查的问题较为复杂,是一次函数和几何知识相结合的问题,同学们要注意几何知识的熟练掌握.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目

 x和y=-
x和y=- x+
x+ .D、E分别为边OC和AB的中点,P为OA边上一动点(点P与点O不重合),连接DE和CP,其交点为Q.
.D、E分别为边OC和AB的中点,P为OA边上一动点(点P与点O不重合),连接DE和CP,其交点为Q.

