题目内容
王强与李刚两位同学在学习“概率”时.做抛骰子(均匀正方体形状)实验,他们共抛了54次,出现向上点数的次数如下表:
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 6 | 9 | 5 | 8 | 16 | 10 |
(2)王强说:“根据实验,一次试验中出现向上点数为5的概率最大.”李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李刚说法的对错;
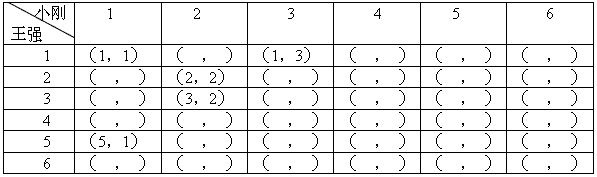
(3)如果王强与李刚各抛一枚骰子.求出现向上点数之和为3的倍数的概率.
 解:(1)向上点数为3的频率=
解:(1)向上点数为3的频率= ;
;向上点数为5的频率=
 ;
;(2)王强的说法不对;李刚的说法不对.
点数为5向上的概率为
 ,
,如果抛540次,那么出现向上点数为6的次数正大约是540×
 =90次;
=90次;(3)由表可知共有36种可能结果,其中和为3的倍数的有12种,
∴P(点数之和为3的倍数)=
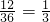 .
.分析:(1)利用频数除以总数即可得到频率;
(2)由于骰子是均匀的,每一面向上的概率均为
 ;
;(3)列举出所有情况,让向上点数之和为3的倍数的情况数除以总情况数即为所求的概率.
点评:本题考查了概率公式和概率的意义,由于骰子是均匀的,与试验次数无关.

练习册系列答案
相关题目
王强与李刚两位同学在学习“概率”时.做抛骰子(均匀正方体形状)实验,他们共抛了54次,出现向上点数的次数如下表:
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率;
(2)王强说:“根据实验,一次试验中出现向上点数为5的概率最大.”李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李刚说法的对错;
(3)如果王强与李刚各抛一枚骰子.求出现向上点数之和为3的倍数的概率.
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 6 | 9 | 5 | 8 | 16 | 10 |
(2)王强说:“根据实验,一次试验中出现向上点数为5的概率最大.”李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李刚说法的对错;
(3)如果王强与李刚各抛一枚骰子.求出现向上点数之和为3的倍数的概率.
王强与李刚两位同学在学习“概率”时,做抛骰子(均匀正方体形状)实验,他们共抛了54次,出现向上点数的次数如下表:
王强说:“根据实验,一次试验中出现向上点数为5的概率最大.”
李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”
请判断王强和李刚说法的对错.
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 6 | 9 | 5 | 8 | 16 | 10 |
李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”
请判断王强和李刚说法的对错.
王强与李刚两位同学在学习“概率”时.做抛骰子(均匀正方体形状)实验,他们共抛了54次,出现向上点数的次数如下表:
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率;
(2)王强说:“根据实验,一次试验中出现向上点数为5的概率最大.”李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李刚说法的对错;
(3)如果王强与李刚各抛一枚骰子.求出现向上点数之和为3的倍数的概率.
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 6 | 9 | 5 | 8 | 16 | 10 |
(2)王强说:“根据实验,一次试验中出现向上点数为5的概率最大.”李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李刚说法的对错;
(3)如果王强与李刚各抛一枚骰子.求出现向上点数之和为3的倍数的概率.
王强与李刚两位同学在学习“概率”时.做抛骰子(均匀正方体形状)实验,他们共抛了54次,出现向上点数的次数如下表:
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率;
(2)王强说:“根据实验,一次试验中出现向上点数为5的概率最大.”李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李刚说法的对错;
(3)如果王强与李刚各抛一枚骰子.求出现向上点数之和为3的倍数的概率.
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 6 | 9 | 5 | 8 | 16 | 10 |
(2)王强说:“根据实验,一次试验中出现向上点数为5的概率最大.”李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李刚说法的对错;
(3)如果王强与李刚各抛一枚骰子.求出现向上点数之和为3的倍数的概率.
