题目内容
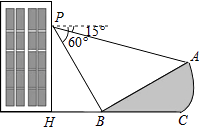
【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

【答案】AD, BE, 同位角相等,两直线平行, BD, CE, 内错角相等,两直线平行, AD, BE, 同旁内角互补,两直线平行, D, 内错角相等,两直线平行, C, 同旁内角互补,两直线平行
【解析】
根据平行线的判定方法解答即可.
(1)若∠4=∠3,则_AD__∥__BE__,理由是;(同位角相等,两直线平行);
(2)若∠2=∠E,则__BD__∥_CE__,理由是(内错角相等,两直线平行);
(3)若∠A=∠ABE=180°,则_AD___∥__BE_,理由是(同旁内角互补,两直线平行);
(4)若∠2=∠_D___,则DA∥EB,理由是(内错角相等,两直线平行);
(5)若∠DBC+∠_C_=180°,则DB∥EC,理由是(同旁内角互补,两直线平行);
故答案为:(1). AD (2). BE (3). 同位角相等,两直线平行; (4). BD, (5)CE, (6)内错角相等,两直线平行; (7). AD, (8)BE, (9)同旁内角互补,两直线平行; (10). D (11). 内错角相等,两直线平行; (12).C, (13) 同旁内角互补,两直线平行.

 同步轻松练习系列答案
同步轻松练习系列答案【题目】已知某品牌的饮料有大瓶装与小瓶装之分.某超市花了3800元购进一批该品牌的饮料共1000瓶,其中大瓶和小瓶饮料的进价及售价如下表所示:
大瓶 | 小瓶 | |
进价(元/瓶) | 5 | 2 |
售价(元/瓶) | 7 | 3 |
(1)该超市购进大瓶和小瓶饮料各多少瓶?
(2)在大瓶饮料售出200瓶,小瓶饮料售出100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?