题目内容
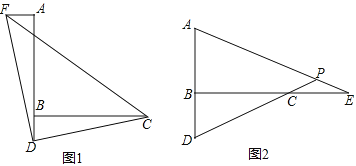
【题目】如图,△ABC内接于⊙O,AD是△ABC的高,⊙O的直径AE交BC于点F,点P在BC的延长线上,∠CAP=∠B。

(1)求证:PA是⊙O的切线;
(2)求证:PCPB=PDPF。
【答案】(1)、证明过程见解析;(2)、证明过程见解析.
【解析】
试题分析:(1)、连接EC,根据∠CAP=∠B得出∠E=∠B=∠CAP,根据直径得出∠ECA=90°,从而说明∠EAP=90°,得出答案;(2)、根据∠P=∠P,∠CAP=∠B得出△PAC∽△PBC,从而得到PA2=PBPC,根据∠P=∠P,∠ADP=∠FAP得出△ADP∽△FAP,从而说明AP2=DPPF,根据两个等式得出答案.
试题解析:(1)、连接EC,
∵∠CAP=∠B,
∴∠E=∠B=∠CAP,
∵⊙O的直径AE,
∴∠ECA=90°,
∴∠E+∠EAC=90°,
∴∠EAC+∠CAP=90°,
∴∠EAP=90°,
∴PA是⊙O的切线;
(2)、∵∠P=∠P,∠CAP=∠B,
∴△PAC∽△PBC,
∴![]() ,
,
∴PA2=PBPC,
∵∠P=∠P,∠ADP=∠FAP,
∴△ADP∽△FAP,
∴![]() ,
,
∴AP2=DPPF,
∴PCPB=PDPF.

练习册系列答案
相关题目