题目内容
【题目】如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,D,E分别是AB,AC边的中点,将△ABC绕点B顺时针旋转60°到△A′BC′的位置,则整个旋转过程中线段DE所扫过部分的面积(即图中阴影部分面积)为_____.

【答案】![]() .
.
【解析】
根据30°角所对的直角边等于斜边的一半求出AB的长度,再根据勾股定理求出AC的长度,然后根据中点定义求出DB、CE的长度,再利用勾股定理求出BE的长度,然后根据旋转变换的性质可得阴影部分的面积等于以BE为半径的扇形面积减去以DB为半径的扇形的面积,然后列式进行计算即可得解.
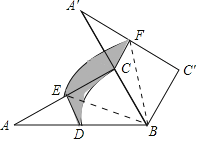
解:连接BE、BF,如右图所示,
∵Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,
∴AB =2BC=12,∴AC=6![]() ,
,
∵D,E分别是AB,AC边的中点,
∴EC=![]() AC=3
AC=3![]() ,BD=BC=
,BD=BC=![]() AB=6,
AB=6,
在Rt△BCE中,根据勾股定理得:BE=3![]() ,
,
∴图中阴影部分面积是:![]() -
-![]() =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目